题目内容
18. 将三角形纸片(△ABC)按如图所示的方式折叠,使点C落在AB边上的点D,折痕为EF.已知AB=AC=3,BC=4,若以点B、D、F为顶点的三角形与△ABC相似,那么CF的长度是( )
将三角形纸片(△ABC)按如图所示的方式折叠,使点C落在AB边上的点D,折痕为EF.已知AB=AC=3,BC=4,若以点B、D、F为顶点的三角形与△ABC相似,那么CF的长度是( )| A. | 2 | B. | $\frac{12}{7}$或2 | C. | $\frac{12}{7}$ | D. | $\frac{12}{5}$或2 |
分析 根据折叠得到FD=CF,设CF=x,则BF=4-x,以点B、D、F为顶点的三角形与△ABC相似,分两种情况:①∠BFD=∠C,②∠BFD=∠A,由三角形相似的性质得出比例式,解方程即可求出x的长,即可选出答案.
解答 解:∵△ABC沿EF折叠C和D重合,
∴FD=CF,
设CF=x,则BF=4-x,
以点B、D、F为顶点的三角形与△ABC相似,分两种情况:
①若∠BFD=∠C,
则$\frac{FD}{BF}$=$\frac{AC}{BC}$,
即$\frac{x}{4-x}$=$\frac{3}{4}$,
解得:x=$\frac{12}{7}$;
②若∠BFD=∠A,
则$\frac{FD}{BF}$=$\frac{AC}{AB}$=1,
即:$\frac{x}{4-x}$=1,
解得:x=2.
综上所述,CF的长为$\frac{12}{7}$或2.
故选:B.
点评 本题主要考查了相似三角形的性质,折叠问题,解一元一次方程等知识点;解此题的关键是设CF=x,能正确列出方程.

练习册系列答案
相关题目
16.把2ab2-4ba+2a分解因式的结果是( )
| A. | 2ab(b-2)+2a | B. | 2a(b2-2b) | C. | 2a(b+1)(b-1) | D. | 2a(b-1)2 |
9. 如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
 如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
13.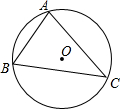 如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )
 如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )| A. | 4 | B. | 3 | C. | 2 | D. | $\sqrt{3}$ |
10.某土建工程共需动用15台挖运机械,每台机械每分钟能挖土3m3或者运土2m3.为了使挖土和运土工作同时结束,安排了x台机械运土,这里x应满足的方程是( )
| A. | 2x=3(15-x) | B. | 3x-2x=15 | C. | 15-2x=3x | D. | 3x=2(15-x) |
 如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F.
如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F. 如图,△ABC中,D、E分别为AB、AC的中点,过点C作AB的平行线交DE的延长线于F点.
如图,△ABC中,D、E分别为AB、AC的中点,过点C作AB的平行线交DE的延长线于F点.