题目内容
1.(1)计算:(-1)2013+|1-${{({-\frac{1}{2}})}^{-2}}}$|-22-(π-2013)0;(2)计算:(2x+y)2-(3x+y)(3x-y)+5x(x-y);
(3)先化简,再求值:[(x-2y)2-(x-y)(3x+y)-5y2]÷2x,其中x=-2,y=1.
分析 (1)先算乘方,再算加减即可;
(2)先算乘法,再合并同类项即可;
(3)先算乘法,再合并同类项,算除法,代入求出即可.
解答 解:(1)解:原式=-1+|1-4|-4-1
=-1+3-4-1
=-3;
(2)原式=4x2+4xy+y2-(9x2-y2)+(5x2-5xy)
=4x2+4xy+y2-9x2+y2+5x2-5xy
=2y2-xy;
(3)原式=[(x2-4xy+4y2)-(3x2-2xy-y2)-5y2]÷2x
=[x2-4xy+4y2-3x2+2xy+y2-5y2]÷2x
=(-2x2-2xy)÷2x
=-x-y,
当x=-2,y=1时,原式=-(-2)-1=1.
点评 本题考查了零指数幂,负整数指数幂,有理数的混合运算,整式的混合运算和求值的应用,能正确运用法则进行计算和化简是解此题的关键,注意:运算顺序.

练习册系列答案
相关题目
11.已知:点A(1,4),点C(1,1),点B(3,1).
(1)如果一次函数y=kx-2的图象与△ACB有交点,求k的取值范围;
(2)如果一次函数y=3x+b的图象与△ACB有交点,求b的取值范围.
(1)如果一次函数y=kx-2的图象与△ACB有交点,求k的取值范围;
(2)如果一次函数y=3x+b的图象与△ACB有交点,求b的取值范围.
16.一个等腰三角形的两边长分别为3,6,则这个等腰三角形的周长是( )
| A. | 12 | B. | 12或15 | C. | 15 | D. | 无法确定 |
6.要使分式$\frac{1}{x-1}$有意义,则x应满足的条件是( )
| A. | x≠1 | B. | x≠-1 | C. | x≠0 | D. | x>1 |
11.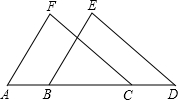 如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )
如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )
 如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )
如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )| A. | AF∥BE | B. | CF∥DE | C. | AB=CD | D. | ∠ACF=∠EBD |
 如图,把一副三角板如图摆放,点E在边AC上,将图中的△ABC绕点A按每秒5°速度沿顺时针方向旋转一周,在旋转的过程中,在第21或57秒时,边BC恰好与边DE平行.
如图,把一副三角板如图摆放,点E在边AC上,将图中的△ABC绕点A按每秒5°速度沿顺时针方向旋转一周,在旋转的过程中,在第21或57秒时,边BC恰好与边DE平行.