题目内容
7.观察下列等式:第1个等式:a1=$\frac{1}{1+\sqrt{2}}$=$\sqrt{2}$-1,
第2个等式:a2=$\frac{1}{\sqrt{2}+\sqrt{3}}$=$\sqrt{3}-\sqrt{2}$,
第3个等式:a3=$\frac{1}{\sqrt{3}+2}$=2-$\sqrt{3}$,
第4个等式:a4=$\frac{1}{2+\sqrt{5}}$=$\sqrt{5}$-2,
…
按上述规律,计算a1+a2+a3+…+an=$\sqrt{n+1}$-$\sqrt{n}$.
分析 首先根据题意,可得:a1+a2+a3+…+an=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$,然后根据分母有理数化的方法,求出算式的值是多少即可.
解答 解:第1个等式:a1=$\frac{1}{1+\sqrt{2}}$=$\sqrt{2}$-1,
第2个等式:a2=$\frac{1}{\sqrt{2}+\sqrt{3}}$=$\sqrt{3}-\sqrt{2}$,
第3个等式:a3=$\frac{1}{\sqrt{3}+2}$=2-$\sqrt{3}$,
第4个等式:a4=$\frac{1}{2+\sqrt{5}}$=$\sqrt{5}$-2,
…
a1+a2+a3+…+an
=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$
=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$
=$\sqrt{n+1}$-$\sqrt{n}$.
故答案为:$\sqrt{n+1}$-$\sqrt{n}$.
点评 此题主要考查了分母有理化的方法,要熟练掌握,解答此题的关键是要明确:分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
2. 如图,OD⊥AB,垂足为点O,OE平分∠AOC,∠DOE=40°,则∠COD的度数是( )
如图,OD⊥AB,垂足为点O,OE平分∠AOC,∠DOE=40°,则∠COD的度数是( )
 如图,OD⊥AB,垂足为点O,OE平分∠AOC,∠DOE=40°,则∠COD的度数是( )
如图,OD⊥AB,垂足为点O,OE平分∠AOC,∠DOE=40°,则∠COD的度数是( )| A. | 10° | B. | 20° | C. | 40° | D. | 80° |
12.下列选项正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{{(-2)}^{2}}$=-2 | ||
| C. | $\root{3}{-125}$=-5 | D. | -1的算术平方根是1 |
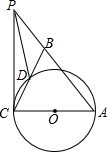 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC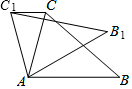 如图,在△ABC中,∠CAB=80°,在同一平面内,将△ABC绕点A旋转到△AB1C1的位置,使得CC1∥AB,求∠BAB1的度数.
如图,在△ABC中,∠CAB=80°,在同一平面内,将△ABC绕点A旋转到△AB1C1的位置,使得CC1∥AB,求∠BAB1的度数.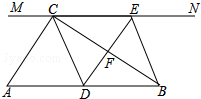 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.