题目内容
17.已知,BC∥OA,∠B=∠A=100°,试回答下列问题:(1)如图1所示,求证:OB∥AC;
(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数;
(3)在(2)的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
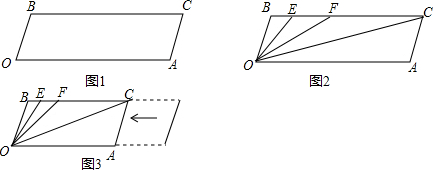
分析 (1)由同旁内角互补,两直线平行证明.
(2)由∠FOC=∠AOC,并且OE平分∠BOF得到∠EOC=∠EOF+∠FOC=$\frac{1}{2}$(∠BOF+∠FOA)=$\frac{1}{2}$∠BOA,算出结果.
(3)先得出结论:∠OCB:∠OFB的值不发生变化,理由为:由BC与AO平行,得到一对内错角相等,由∠FOC=∠AOC,等量代换得到一对角相等,再利用外角性质等量代换即可得证;
解答 解:(1)∵BC∥OA,
∴∠B+∠O=180°,又∵∠B=∠A,
∴∠A+∠O=180°,
∴OB∥AC;
(2)∵∠B+∠BOA=180°,∠B=100°,
∴∠BOA=80°,
∵OE平分∠BOF,
∴∠BOE=∠EOF,
又∵∠FOC=∠AOC,
∴∠EOF+∠FOC=$\frac{1}{2}$(∠BOF+∠FOA)=$\frac{1}{2}$∠BOA=40°;
(3)结论:∠OCB:∠OFB的值不发生变化.理由为:
∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
点评 此题考查了平行线的判定与性质,平移的性质,以及角的计算,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.分别满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三边之比为1:$\sqrt{2}$:$\sqrt{3}$ | B. | 三边长依次为9,40,41 | ||
| C. | 三内角之比为3:4:5 | D. | 三内角之比为1:1:2 |
7.下列利用乘法公式运算中错误的是( )
| A. | (-a+b)(-a-b)=a2-b2 | B. | (-a-b)2=a2+b2+2ab | C. | (-a+b)2=a2+b2-2ab | D. | (-a-b)(a+b)=a2-b2 |
 如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,点O到BC边的距离为3,且△ABC的周长为20,则△ABC的面积为30.
如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,点O到BC边的距离为3,且△ABC的周长为20,则△ABC的面积为30.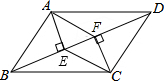 已知:如图,在?ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE,求证:AF∥EC.
已知:如图,在?ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE,求证:AF∥EC.
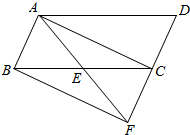 如图,已知点E是?ABCD中BC边的中点,若∠ABE=∠BAE=60°,BC=4,连接AE并延长交DC的延长线于点F.
如图,已知点E是?ABCD中BC边的中点,若∠ABE=∠BAE=60°,BC=4,连接AE并延长交DC的延长线于点F.