题目内容
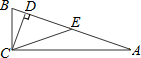 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,点E是AB中点,AB=10,则线段DE的长度为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,点E是AB中点,AB=10,则线段DE的长度为( )| A、3 | ||||
| B、5 | ||||
C、5
| ||||
D、
|
考点:等腰直角三角形,直角三角形斜边上的中线
专题:
分析:利用CD、CE分别为斜边AB上的高和中线可得:“∠B=∠ECB,∠ACD=∠ECB”,再利用∠BCD与∠ACD之比为3:1即可求得∠ECD的大小,证得△CDE为等腰直角三角形.利用勾股定理可以求得CE=DE=
CE=
×
AB.
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:解:∵∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B,
又∵CE是直角△ABC的斜边AB上的中线,
∴CE=EB,∠B=∠ECB,∠ACD=∠ECB,
但∵∠BCD=3∠ACD,
∠ECD=2∠ACD=
∠ACB=
×90°=45°,
∴△EDC为等腰直角三角形,
∴CE=DE=
CE=
×
AB=
.
故选:D.
∴∠ACD=∠B,
又∵CE是直角△ABC的斜边AB上的中线,
∴CE=EB,∠B=∠ECB,∠ACD=∠ECB,
但∵∠BCD=3∠ACD,
∠ECD=2∠ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∴△EDC为等腰直角三角形,
∴CE=DE=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
5
| ||
| 2 |
故选:D.
点评:本小题主要考查直角三角形中边角关系、三角形高和中线等基础知识,考查运算求解能力、转化思想.属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
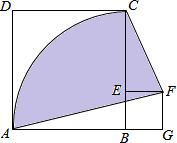 如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为( )
如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为( )| A、2π | B、4π |
| C、4π-2 | D、6π |
计算(-
)-2的结果是( )
| 1 |
| 3 |
| A、9 | ||
| B、-9 | ||
C、-
| ||
D、
|
 已知平行四边形ABCD中,E为AD的中点,AF:BF=2:3,求AG:GC的值.
已知平行四边形ABCD中,E为AD的中点,AF:BF=2:3,求AG:GC的值.