题目内容
11.若点E,F,G,H分别是菱形ABCD的边AB,BC,CD,DA的中点,则四边形EFGH的形状为矩形.分析 连接AC、BD交于O,根据三角形的中位线定理推出EF∥BD∥HG,EH∥AC∥FG,得出四边形EFGH是平行四边形,根据菱形性质推出AC⊥BD,推出EF⊥EH,即可得出答案.
解答 解:四边形EFGH的形状为矩形,
理由如下:
连接AC、BD交于O,
∵E、F、G、H分别是AB、AD、CD、BC的中点,
∴EF∥BD,FG∥AC,HG∥BD,EH∥AC,
∴EF∥HG,EH∥FG,
∴四边形EFGH是平行四边形,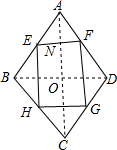
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EF∥BD,EH∥AC,
∴EF⊥EH,
∴∠FEH=90°,
∴平行四边形EFGH是矩形,
故答案为:矩形.
点评 本题考查了矩形的判定,菱形的性质,平行四边形的判定,平行线性质等知识点的运用,主要考查学生能否正确运用性质进行推理,题目比较典型,难度适中.

练习册系列答案
相关题目
19.若不等式组$\left\{\begin{array}{l}{x-a>0}\\{x-a<1}\end{array}\right.$的解集中的任何一个x的值均不在2≤x≤5范围内,则a的取值范围是( )
| A. | a<1 | B. | a<1或a>5 | C. | a≤1或a≥5 | D. | a<1且a>5 |
6.已知点(-2,y1),(-1,y2),(1,y3)都在直线y=-3x+2上,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y3>y2>y1 | D. | y3<y2<y1 |
16.A、B、C、D、E五名学生在一次语文测验中的平均成绩是80分,而A、B、C三同学的平均成绩是78分,那么下列说法一定正确的是( )
| A. | D、E的成绩比其他三个都好 | B. | D、E两人的平均成绩是82分 | ||
| C. | 最高分得主不是A、B、C、D | D. | D、E中至少有一个成绩不少于83分 |