题目内容
1.直线y=k1x+b1与y=k2x+b2(k1k2<0)相交于点A(-2,0),且两直线与y轴围成的三角形面积为4,求b1-b2的值.分析 分类讨论:当k1>0,k2<0时,直线y=k1x+b1与y轴交于B点,则B(0,b1),直线y=k2x+b2与y轴交于C点,则C(0,b2),根据三角形面积公式得到$\frac{1}{2}$×2×(b1-b2)=4,则b1-b2=4;当k1<0,k2>0时,易得b1-b2=-4.
解答 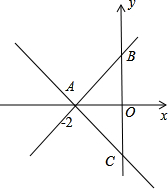 解:如图,当k1>0,k2<0时,直线y=k1x+b1与y轴交于B点,则B(0,b1),直线y=k2x+b2与y轴交于C点,则C(0,b2),
解:如图,当k1>0,k2<0时,直线y=k1x+b1与y轴交于B点,则B(0,b1),直线y=k2x+b2与y轴交于C点,则C(0,b2),
∵△ABC的面积为4,
∴$\frac{1}{2}$OA(OB+OC)=4,
即$\frac{1}{2}$×2×(b1-b2)=4,
∴b1-b2=4;
当k1<0,k2>0时,同理可得b1-b2=-4,
∴b1-b2的值为±4.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
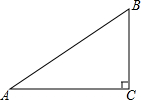 如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8,求AC的长.
如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8,求AC的长. 一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在白色方格地面上的概率是$\frac{3}{4}$.
一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在白色方格地面上的概率是$\frac{3}{4}$.