题目内容
19.设x为实数,下列式子成立的是( )| A. | $\sqrt{{x}^{2}}$=($\sqrt{x}$)2 | B. | $\root{3}{{x}^{3}}$=$\sqrt{{x}^{2}}$ | C. | $\sqrt{{(-x)}^{2}}$=|-x| | D. | $\sqrt{{x}^{2}-4}$=$\sqrt{x+2}$•$\sqrt{x-2}$ |
分析 依据立方根和算术平方根的性质,二次根式的乘法法则求解即可.
解答 解:A、当x<0时,$\sqrt{x}$无意义,故A错误;
B、当$\root{3}{{x}^{3}}$=x,$\sqrt{{x}^{2}}$=|x|,当x<0时,不成立,故B错误;
C、$\sqrt{(-x)^{2}}$=|-x|是正确的;
D、当x+2<0或x-2<0时,$\sqrt{{x}^{2}-4}$=$\sqrt{x+2}$•$\sqrt{x-2}$不成立,故D错误.
故选:D.
点评 本题考查了立方根和算术平方根,二次根式的乘法法则的条件.关键是要求等式左右两边的被开方数为非负数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如果一个四边形绕对角线的交点旋转90°后,所得图形与原来的图形重合,那么这个四边形是( )
| A. | 正方形 | B. | 菱形 | ||
| C. | 矩形 | D. | 对角线垂直的任意四边形 |
 如图,AB是⊙O的直径,CD切⊙O于C,AD⊥CD于D.求证:AC平分∠DAB.
如图,AB是⊙O的直径,CD切⊙O于C,AD⊥CD于D.求证:AC平分∠DAB.
 中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示)
中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示) 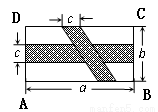
 已知:抛物线y=ax2+bx+c的图象如图所示,则a的取值范围是a<0.
已知:抛物线y=ax2+bx+c的图象如图所示,则a的取值范围是a<0.
 如图,⊙O的内接四边形ABCD中,∠A=110°,则∠BOD等于140°.
如图,⊙O的内接四边形ABCD中,∠A=110°,则∠BOD等于140°. 如图,用十字形方框从日历表中框出5个数,已知这5个数的和为5a-5,a是方框①,②,③,④中的一个数,则数a所在的方框是( )
如图,用十字形方框从日历表中框出5个数,已知这5个数的和为5a-5,a是方框①,②,③,④中的一个数,则数a所在的方框是( )