题目内容
4.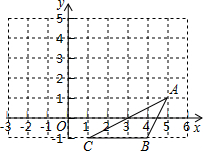 已知,△ABC在直角坐标系中的位置如图所示,现将△ABC先向上平移3个单位,再向左平移2个单位.
已知,△ABC在直角坐标系中的位置如图所示,现将△ABC先向上平移3个单位,再向左平移2个单位.(1)画出两次平移后△ABC的位置(用△ABC表示);
(2)写出△A1B1C1各顶点的坐标;
(3)求△AA1B1的面积.
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用(1)中所画图形得出各点坐标即可;
(3)利用△AA1B1所在矩形面积减去周围三角形面积进而得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)A1(3,4),B1(2,2),C1(-1,2);
(3)△AA1B1的面积为:3×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×1=3.5.
点评 此题主要考查了平移变换以及三角形面积求法,正确得出平移后对应点位置是解题关键.

练习册系列答案
相关题目
19.下列命题中,是假命题的是( )
| A. | 对顶角相等 | |
| B. | 同位角相等 | |
| C. | 垂线段最短 | |
| D. | 平行于同一直线的两条直线也互相平行 |
9.菱形ABCD的周长为24cm,其中一条对角线的长为8cm,则菱形ABCD的面积为( )
| A. | 8$\sqrt{5}$cm2 | B. | 16$\sqrt{5}$cm2 | C. | 32$\sqrt{5}$cm2 | D. | 48cm2 |
16.下列各式能运用公式法进行因式分解的有( )个
(1)-a2+b2
(2)16m2-25n2
(3)9p2-24pq+16q2
(4)(a+b)2+a+b+$\frac{1}{4}$.
(1)-a2+b2
(2)16m2-25n2
(3)9p2-24pq+16q2
(4)(a+b)2+a+b+$\frac{1}{4}$.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
14.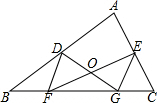 如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
 如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |