题目内容
15.已知关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0(Ⅰ)求证:方程有两个不相等的实数根;
(Ⅱ)若△ABC的两边AB、AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求△ABC的周长.
分析 (1)要证明无论k为何值时,方程总有两个不相等的实数根,就是证明△>0,而△=(2k+3)2-4(k2+3k+2)=1,所以△>0;
(2)根据等腰三角形的性质,分三种情况讨论:①AB=AC,②AB=BC,③BC=AC;后两种情况相同,则可分两种情况,再由根与系数的关系得出k的值.
解答 (1)证明:∵△=(2k+3)2-4(k2+3k+2)=1,
∴△>0,
∴无论k取何值时,方程总有两个不相等的实数根;
(2﹚解:∵△ABC是等腰三角形;
∴当AB=AC时,△=b2-4ac=0,
∴(2k+3)2-4(k2+3k+2)=0,
解得k不存在;
当AB=BC时,即AB=5,
∴5+AC=2k+3,5AC=k2+3k+2,
解得k=3或4,
∴AC=4或6.
∴△ABC的周长为14或16.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次方程的解法.

练习册系列答案
相关题目
10.下列函数中,y是x的正比例函数的是( )
| A. | y=kx | B. | y=2x-1 | C. | y=$\sqrt{2}$x | D. | y=2x2 |
7.能够用立方和(差)公式进行计算的是( )
| A. | (m+n)(m3+m2n+n3) | B. | (m-n)(m2+n2) | C. | (x+1)(x2-x+1) | D. | (x2+1)(x2-x+1) |
5. 如图,∠A=50°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
如图,∠A=50°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
 如图,∠A=50°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
如图,∠A=50°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图,有两条笔直的公路(BD和EF,其宽度不计)从一块矩形的土地ABCD中穿过,EF是BD的垂直平分线,有BD=400m,EF=300m,求这块矩形土地ABCD的面积是76800m2.
如图,有两条笔直的公路(BD和EF,其宽度不计)从一块矩形的土地ABCD中穿过,EF是BD的垂直平分线,有BD=400m,EF=300m,求这块矩形土地ABCD的面积是76800m2. 如图,△AOB是等边三角形,且B(2,0),OC是AB边的中线,将△AOB绕点O逆时针旋转120°得到△A1OB1.
如图,△AOB是等边三角形,且B(2,0),OC是AB边的中线,将△AOB绕点O逆时针旋转120°得到△A1OB1.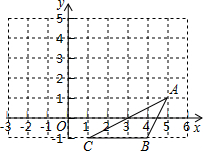 已知,△ABC在直角坐标系中的位置如图所示,现将△ABC先向上平移3个单位,再向左平移2个单位.
已知,△ABC在直角坐标系中的位置如图所示,现将△ABC先向上平移3个单位,再向左平移2个单位.