题目内容
14.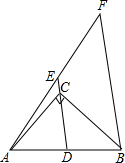 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.
分析 根据直角三角形斜边上的中线等于斜边的一半得到CD=$\frac{1}{2}$AB=3,结合已知条件CE=$\frac{1}{3}$CD可以求得ED=4.然后由三角形中位线定理可以求得BF=2ED=8.
解答  解:如图,∵∠ACB=90°,D为AB的中点,AB=6,
解:如图,∵∠ACB=90°,D为AB的中点,AB=6,
∴CD=$\frac{1}{2}$AB=3.
又∵CE=$\frac{1}{3}$CD,
∴CE=1,
∴ED=CE+CD=4.
又∵BF∥DE,点D是AB的中点,
∴ED是△AFB的中位线,
∴BF=2ED=8.
故答案为:8.
点评 本题考查了三角形中位线定理和直角三角形斜边上的中线.根据已知条件求得ED的长度是解题的关键与难点.

练习册系列答案
相关题目
 抛物线y=x2+bx+c与x轴分别交于点A(-1,0)和点B,与y轴的交点C坐标为(0,-3).
抛物线y=x2+bx+c与x轴分别交于点A(-1,0)和点B,与y轴的交点C坐标为(0,-3). 如图,∠AOB=35°,∠BOC=90°,OD是∠AOC的平分线,求∠BOD的度数.
如图,∠AOB=35°,∠BOC=90°,OD是∠AOC的平分线,求∠BOD的度数. 如图,若AB∥CD,则∠α=150°,∠β=80°,则∠γ=50°.
如图,若AB∥CD,则∠α=150°,∠β=80°,则∠γ=50°.