题目内容
17.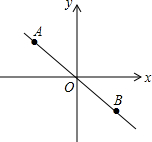 如图,A,B是正比例函数y=-$\frac{3}{4}$x图象上的两点,点A的坐标是(-4,3),点B的坐标是(4.-3),若点P是x轴上一点,且S△APB=15,求点P的坐标.
如图,A,B是正比例函数y=-$\frac{3}{4}$x图象上的两点,点A的坐标是(-4,3),点B的坐标是(4.-3),若点P是x轴上一点,且S△APB=15,求点P的坐标.
分析 根据x轴上点的坐标特征,可设P点坐标为(t,0),再根据三角形面积公式得到$\frac{1}{2}$•(3+3)•|t|=15,然后解方程求出t即可得到P点坐标.
解答 解:设P点坐标为(t,0),
∵S△APB=15,
∴$\frac{1}{2}$•|t|•(3+3)=15,
∴t=±5,
∴P点坐标为(5,0)或(-5,0).
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线;直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.下列计算正确的是( )
| A. | x3+x2=x5 | B. | x6÷x3=x2 | C. | x3•x2=x5 | D. | (x3)2=x5 |
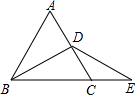 如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.
如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.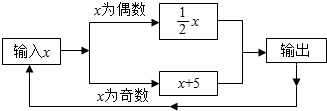 有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2015次输出的结果是4.
有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2015次输出的结果是4.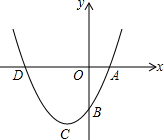 如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).
如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).