题目内容
20.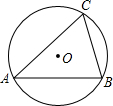 如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.
如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.
分析 首先作⊙O的直径CD,连接BD,可得∠CBD=90°,由已知条件得出△BCD是等腰直角三角形,得出CD=$\sqrt{2}$BC=4$\sqrt{2}$即可.
解答 解:作⊙O的直径CD,连接BD,如图所示:
则∠CBD=90°,
∵∠D=∠BAC=45°,
∴△BCD是等腰直角三角形,
∴CD=$\sqrt{2}$BC=4$\sqrt{2}$,
即⊙O的直径为4$\sqrt{2}$.
点评 此题考查了圆周角定理、等腰直角三角形的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目

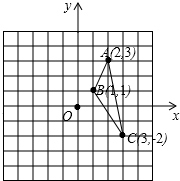 如图,利用关于坐标轴对称的点的坐标特点.
如图,利用关于坐标轴对称的点的坐标特点.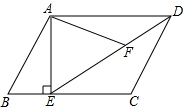 如图,在平行四边形ABCD中,过点F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点F为线段DE上一点,且∠AFE=∠B.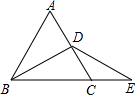 如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.
如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.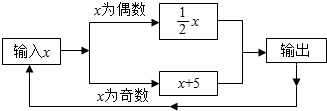 有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2015次输出的结果是4.
有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2015次输出的结果是4.