题目内容
3. 在平面直角坐标系中,点A(0,6),点B(t,0)是x轴正半轴上的点,连结AB,取AB的中点M,将线段MB绕着点B按顺时针方向旋转90°,得到线段BC.
在平面直角坐标系中,点A(0,6),点B(t,0)是x轴正半轴上的点,连结AB,取AB的中点M,将线段MB绕着点B按顺时针方向旋转90°,得到线段BC.(1)点C的坐标为(t+3,$\frac{t}{2}$);
(2)△ABC的面积为$\frac{{t}^{2}+36}{4}$.(均用含t的代数式表示)
分析 (1)根据点A和点B的坐标可以求得点M的坐标,从而可以求得点C的坐标;
(2)根据点A和点B的坐标可以求得AB的长,从而可以求得BM的长,进而求得△ABC的面积.
解答 解:(1)∵点A(0,6),点B(t,0),点M是线段AB的中点,
∴点M的坐标是($\frac{t}{2},3$),
又∵将线段MB绕着点B按顺时针方向旋转90°,得到线段BC,
∴点C的坐标为:(t+3,$\frac{t}{2}$),
故答案为:(t+3,$\frac{t}{2}$);
(2)∵点A(0,6),点B(t,0),点M的坐标是($\frac{t}{2},3$),∠ABC=90°,
∴AB=$\sqrt{{t}^{2}+36}$,BM=$\frac{1}{2}AB$=$\frac{\sqrt{{t}^{2}+36}}{2}$,
∴BC=$\frac{\sqrt{{t}^{2}+36}}{2}$,
∴△ABC的面积是:$\frac{AB•BC}{2}=\frac{\sqrt{{t}^{2}+36}•\frac{\sqrt{{t}^{2}+36}}{2}}{2}=\frac{{t}^{2}+36}{4}$,
故答案为:$\frac{{t}^{2}+36}{4}$.
点评 本题考查坐标与图形的变化-旋转,三角形的面积,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
14.三角形的三条边长分别为a,b,c,满足等式(a+b)2-c2=2ab,则此三角形是( )
| A. | 锐角三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 钝角三角形 |
11.计算-1+2-3+4-5+6…-97+98-99的结果为( )
| A. | -50 | B. | -49 | C. | 49 | D. | 50 |
18.如果一条直线l经过平面内三个不同的点A(m,n),B(-n,-m),C(m+n,m+n),那么直线l不经过( )
| A. | 第二、四象限 | B. | 第一、三象限 | C. | 第一象限 | D. | 第三象限 |
15. 如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )
如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )
 如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )
如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )| A. | 3$\sqrt{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | 6 | D. | 3 |
13.某中学为了解全校的耗电情况,抽查了10天中全校每天的耗电量数据如表(单位:度)
计算该校每天的平均用电量,并估计该校五月分的耗电量为3240度.
| 度数 | 90 | 93 | 102 | 113 | 114 | 120 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
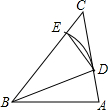 如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,AB长为半径的弧分别交AC,BC于点D,连接BD,ED,若∠CED=105°,求∠ABC的度数为( )
如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,AB长为半径的弧分别交AC,BC于点D,连接BD,ED,若∠CED=105°,求∠ABC的度数为( )