题目内容
4.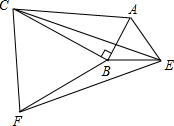 已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC.
已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC.(1)找出图中的全等三角形(不添加辅助线),并证明你的结论;
(2)BE和CF有怎么样的位置关系?
分析 (1)由图可知△CBE与△FBE全等,利用SAS证明即可;
(2)根据全等三角形的性质得出CE=FE,∠FEB=∠CEB,利用等腰三角形的性质解答即可.
解答 解:(1)△CBE≌△FBE,理由如下:
∵以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,
∴∠CBE=90°+60°=150°,∠FBE=360°-90°-60°-60°=150°,
在△CBE与△FBE中,
$\left\{\begin{array}{l}{CB=BF}\\{∠CBE=∠FBE}\\{BE=BE}\end{array}\right.$,
∴△CBE≌△FBE(SAS);
(2)垂直关系,理由如下:
∵△CBE≌△FBE,
∴CE=FE,∠FEB=∠CEB,
∴BE⊥CF.
点评 此题考查全等三角形的判定和性质,关键是利用SAS证明△CBE≌△FBE.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.
如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.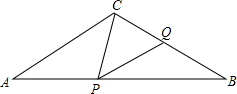 如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y.
如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y. 已知:如图,∠BAC=∠ABD,AC=BD,AD、BC相交于点O,E是AB的中点,试判断OE与AB的位置关系,并给出证明.
已知:如图,∠BAC=∠ABD,AC=BD,AD、BC相交于点O,E是AB的中点,试判断OE与AB的位置关系,并给出证明.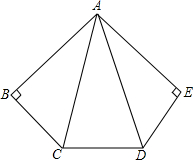 如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED.
如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED.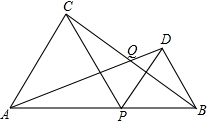 如图,已知线段AB的长为2a,点P是AB上的动点(点P不与A,B重合),分别以AP,PB为边向线段AB的同一侧作等边三角形APC和等边三角形PBD,连接AD,BC相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由.
如图,已知线段AB的长为2a,点P是AB上的动点(点P不与A,B重合),分别以AP,PB为边向线段AB的同一侧作等边三角形APC和等边三角形PBD,连接AD,BC相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由.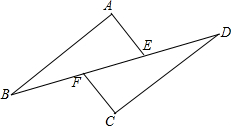 如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明.
如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明.