题目内容
16.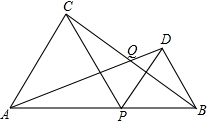 如图,已知线段AB的长为2a,点P是AB上的动点(点P不与A,B重合),分别以AP,PB为边向线段AB的同一侧作等边三角形APC和等边三角形PBD,连接AD,BC相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由.
如图,已知线段AB的长为2a,点P是AB上的动点(点P不与A,B重合),分别以AP,PB为边向线段AB的同一侧作等边三角形APC和等边三角形PBD,连接AD,BC相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由.
分析 首先根据等边三角形的性质得到PA=PC,∠APC=60°,PB=PD,∠BPD=60°,于是得到∠APD=∠CPB,证得△APD≌△CPB,然后根据三角形的外角的性质即可求解.
解答 解:α的大小不会随点P的移动而变化,
理由:∵△APC是等边三角形,
∴PA=PC,∠APC=60°,
∵△BDP是等边三角形,
∴PB=PD,∠BPD=60°,
∴∠APC=∠BPD,
∴∠APD=∠CPB,
在△APD与△CPB中,$\left\{\begin{array}{l}{AP=PC}\\{∠APD=∠CPB}\\{PD=PB}\end{array}\right.$,
∴△APD≌△CPB,
∴∠PAD=∠PCB,
∵∠QAP+∠QAC+∠ACP=120°,
∴∠QCP+∠QAC+∠ACP=120°,
∴∠AQC=180°-120°=60°.
∴α的大小不会随点P的移动而变化.
点评 本题考查了旋转的性质,以及全等三角形的判定与性质,正确证明两个三角形全等是解题的关键.

练习册系列答案
相关题目
8.下面各组中的三条线段能组成三角形的是( )
| A. | 6cm,7cm,12cm | B. | 6cm,8cm,15cm | C. | 8cm,12cm,20cm | D. | 6cm,6cm,13cm |
5.太阳距地球的距离约为15000000千米,用科学记数法表示为( )
| A. | 0.15×109千米 | B. | 1.5×108千米 | C. | 15×107千米 | D. | 1.5×107千米 |
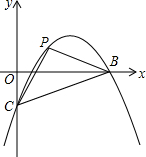 如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.
如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.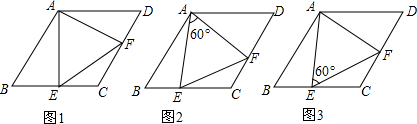
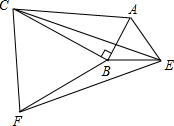 已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC.
已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC. 如图,△ABC,△ADE均为等边三角形,连接BD,CE,则线段BD与CE的数量关系是BD=CE.
如图,△ABC,△ADE均为等边三角形,连接BD,CE,则线段BD与CE的数量关系是BD=CE.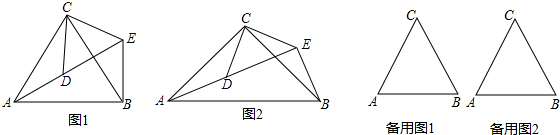
 画出下列几何体的三种形状图.
画出下列几何体的三种形状图.