题目内容
15. 如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.
如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.(1)求△ABC的面积;
(2)设BP=x,QR=y,求y关于x的函数解析式,并指出它的定义域;
(3)连结CQ,△AQR与△QBC是否有可能相似?如果不可能,说明理由;如果可能,求出此时BP的长.
分析 (1)如图1,过A作AM⊥BC交BC于M,根据三角函数求得AM=5$\sqrt{3}$,于是得到S△ABC=$\frac{1}{2}×BC×AM$=$\frac{1}{2}×16×5\sqrt{3}$=40$\sqrt{3}$;
(2)如图2,过Q作QD∥BC交AC于D,根据相似三角形的判定定理得到△AQD∽△ABC,得到比例式$\frac{QD}{BC}=\frac{AQ}{AB}$,求得DQ=$\frac{AQ•BC}{AB}$=$\frac{(10-x)×16}{10}$=16-1.6x,通过△RQD∽△RPC,得到比例式$\frac{QR}{RP}$=$\frac{QD}{PC}$代入数据即可得到结论;
(3)根据对顶角相等得到∠AQR=∠QBC=60°,如果△AQR与△QBC,则有$\frac{AQ}{BQ}=\frac{QR}{BC}$,代入数据即可得到结论.
解答  解:(1)如图1,过A作AM⊥BC交BC于M,
解:(1)如图1,过A作AM⊥BC交BC于M,
∵AB=10,∠B=60°,∴AM=5$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}×BC×AM$=$\frac{1}{2}×16×5\sqrt{3}$=40$\sqrt{3}$;
(2)∵∠B=60°,
∴△BPQ是等边三角形,
如图2,过Q作QD∥BC交AC于D,
∴△AQD∽△ABC,
∴$\frac{QD}{BC}=\frac{AQ}{AB}$,
∴DQ=$\frac{AQ•BC}{AB}$=$\frac{(10-x)×16}{10}$=16-1.6x,
∴△RQD∽△RPC,
∴$\frac{QR}{RP}$=$\frac{QD}{PC}$
∴$\frac{y}{y+x}$=$\frac{16-1.6x}{(16-x)y}$=$\frac{16-1.6x}{0.6y}$,
∴y=-$\frac{8}{3}$x+$\frac{80}{3}$(0<x<10);
(3)∵∠AQR=∠QBC=60°,
如果△AQR与△QBC,
则$\frac{AQ}{BQ}=\frac{QR}{BC}$,
∴$\frac{10-x}{x}=\frac{y}{16}$,
即$\frac{10-x}{x}$=$\frac{-\frac{8}{3}x+\frac{80}{3}}{16}$,
解得:x=6,或x=10(不合题意舍去),
∴当BP=6时,△AQR与△QBC相似.
点评 本题考查了相似三角形的判定和性质,求函数的解析式,等边三角形的性质,求三角形的面积,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 0.15×109千米 | B. | 1.5×108千米 | C. | 15×107千米 | D. | 1.5×107千米 |
 ,则x2﹣y2的值为______.
,则x2﹣y2的值为______.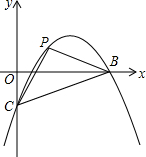 如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.
如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.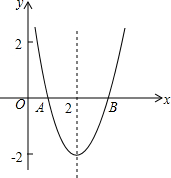 已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根.
已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根. 如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.
如图,AC⊥CB,AD为△ABC的中线,CG为高,DE⊥AD,BC=2AC,求证:AD=DF+DE.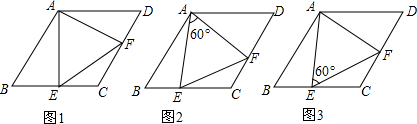
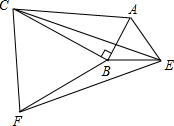 已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC.
已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC.