题目内容
13.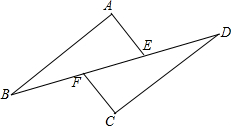 如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明.
如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明.
分析 根据等式的性质得出BE=DF,利用平行线的性质得出∠B=∠D,∠AEB=∠CFD,利用ASA证明△ABE与△DCF全等,进而解答即可.
解答 解:AB=CD,AE=CF,BE=DF,理由如下:
∵BF=DE,
∴BE=DF,
∵AB∥CD,AE∥CF,
∴∠B=∠D,∠AEB=∠CFD,
在△ABE与△DCF中
$\left\{\begin{array}{l}{∠B=∠D}\\{BE=DF}\\{∠AEB=∠CFD}\end{array}\right.$,
∴△ABE≌△DCF(ASA),
∴AB=CD,AE=CF.
点评 此题考查全等三角形的判定和性质,关键是根据等式的性质得出BE=DF.

练习册系列答案
相关题目
8.下面各组中的三条线段能组成三角形的是( )
| A. | 6cm,7cm,12cm | B. | 6cm,8cm,15cm | C. | 8cm,12cm,20cm | D. | 6cm,6cm,13cm |
5.太阳距地球的距离约为15000000千米,用科学记数法表示为( )
| A. | 0.15×109千米 | B. | 1.5×108千米 | C. | 15×107千米 | D. | 1.5×107千米 |
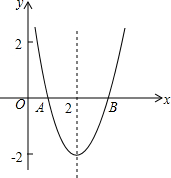 已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根.
已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根.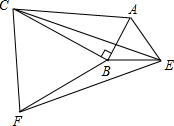 已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC.
已知:如图,分别以Rt△ABC的两条直角边AB,BC为边作等边△ABE和等边△BCF,分别连结EF,EC.