题目内容
17.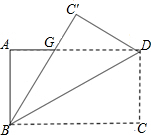 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.(1)求证:BG=DG.
(2)求△BDG的面积.
分析 (1)因为折叠前后∠DBC=∠DBC′,且因为平行,内错角相等,所以∠DCB=∠ADB,所以根据角之间的等量代换可知DG=BG;
(2)要想求出三角形BGD的面积,根据题中条件,只要求出三角形AGB或者GDC′面积后,利用求差的办法即可求得△BGD的面积.
解答 (1)证明:∵△BDC′是由△BDC沿直线BD折叠得到的,
∴∠C′BD=∠CBD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CBD=∠GDB,
∴∠C′BD=∠GDB,
∴BG=DG;
(2)解:设DG=x,则AG=AD-DG=8-x,
∵∠A=90°,BG=DG=x,
∴BG2=AB2+AG2,
∴x2=62+(8-x)2,
∴x=$\frac{25}{4}$,
∴△BGD的面积=$\frac{1}{2}$DG×AB=$\frac{1}{2}$×$\frac{25}{4}$×6=$\frac{75}{4}$(cm).
点评 本题考查了翻折变换的性质,矩形的性质,勾股定理,熟记翻折前后的两个图形能够完全重合得到相等的边和角是解题的关键,(2)利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
8.化简(-a2)5+(-a5)2的结果( )
| A. | -2a7 | B. | 0 | C. | a | D. | -2a10 |
9.下列说法正确的是( )
| A. | 64的立方根是±$\root{3}{64}$=±$\sqrt{4}$ | B. | -$\frac{1}{2}$是-$\frac{1}{6}$的立方根 | ||
| C. | $\root{3}{-27}$=-$\root{3}{27}$ | D. | 立方根等于它本身的数是0和1 |
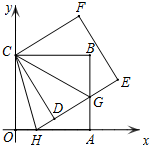 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形OCBA绕点C逆时针旋转角度一个锐角度数α,得到正方形DCFE,ED交线段AB与点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形OCBA绕点C逆时针旋转角度一个锐角度数α,得到正方形DCFE,ED交线段AB与点G,ED的延长线交线段OA于点H,连CH、CG. 如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=30°,则∠2=60°.
如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=30°,则∠2=60°.