题目内容
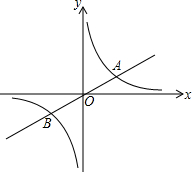 反比例函数y=
反比例函数y=| k |
| x |
| ||
| 3 |
| 6 |
(1)求反比例函数的解析式.
(2)若抛物线y=x2上存在点C,平面内存在点D,使得四边形ACBD是矩形(AB为对角线),求D点的坐标.
(3)若抛物线y=x2+bx+c上存在两点E、F,使得四边形AEBF为菱形(EF为对角线),
①当c=-1时,求b的值.
②要使(3)中满足条件的点E、F存在,求c的范围.
考点:反比例函数综合题
专题:
分析:(1)设A(x,
x),则B(-x,-
x),再根据AB=2
即可得出x的值,进而得出AAB两点坐标,根据点A在反比例函数y=
上求出k的值即可得出其函数解析式;
(2)设D(x,y),再求出OA的长,根据OA=OD即可得出C点坐标,再根据C、D两点关于原点对称即可得出D点坐标;
(3)①根据四边形AEBF为菱形(EF为对角线),直线AB的解析式为y=
x可得出直线EF的解析式,设E(x,-
x),则F(-x,
x),再根据点E、F是直线与二次函数的交点即可得出b的值;
②直接根据菱形的性质即可得出结论.
| ||
| 3 |
| ||
| 3 |
| 6 |
| k |
| x |
(2)设D(x,y),再求出OA的长,根据OA=OD即可得出C点坐标,再根据C、D两点关于原点对称即可得出D点坐标;
(3)①根据四边形AEBF为菱形(EF为对角线),直线AB的解析式为y=
| ||
| 3 |
| 3 |
| 3 |
②直接根据菱形的性质即可得出结论.
解答:解:(1)∵A、B两点在直线y=
x上,
∴A(x,
x),则B(-x,-
x),
∵AB=2
,
∴
=2
,
解得x=±
,
∴A(
,
),B(-
,-
).
∵点A在反比例函数y=
上,
∴k=
×
=
,
∴反比例函数的解析式为:y=
;
(2)设D(x,y),
∵四边形ACBD是矩形(AB为对角线),A(
,
),
∴OA=
=
,
∴OA=OA=
,即
=
,
∵点D在二次函数y=x2上,
∴
=
,解得y=2,
∴C1(
,2),C2(-
,2),
∵C、D两点关于原点对称,
∴D1(
,-2),D2(-
,-2),
(3)①∵四边形AEBF为菱形(EF为对角线),直线AB的解析式为y=
x,
∴EF⊥AB,直线EF的解析式为y=-
x.
∵c=1,
∴二次函数的解析式为y=x2+bx-1,
设E(x,-
x),则F(-x,
x),
∵点E、F是直线与二次函数的交点,
∴
,解得b=-
;
②∵四边形AEBF为菱形(EF为对角线),
∴抛物线y=x2+bx+c一定与x轴有两个交点,
∴c<0.
| ||
| 3 |
∴A(x,
| ||
| 3 |
| ||
| 3 |
∵AB=2
| 6 |
∴
(x+x)2+(
|
| 6 |
解得x=±
3
| ||
| 2 |
∴A(
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
∵点A在反比例函数y=
| k |
| x |
∴k=
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2x |
∴反比例函数的解析式为:y=
3
| ||
| 2x |
(2)设D(x,y),
∵四边形ACBD是矩形(AB为对角线),A(
3
| ||
| 2 |
| ||
| 2 |
∴OA=
(
|
| 6 |
∴OA=OA=
| 6 |
| x2+y2 |
| 6 |
∵点D在二次函数y=x2上,
∴
| y+y2 |
| 6 |
∴C1(
| 2 |
| 2 |
∵C、D两点关于原点对称,
∴D1(
| 2 |
| 2 |
(3)①∵四边形AEBF为菱形(EF为对角线),直线AB的解析式为y=
| ||
| 3 |
∴EF⊥AB,直线EF的解析式为y=-
| 3 |
∵c=1,
∴二次函数的解析式为y=x2+bx-1,
设E(x,-
| 3 |
| 3 |
∵点E、F是直线与二次函数的交点,
∴
|
| 3 |
②∵四边形AEBF为菱形(EF为对角线),
∴抛物线y=x2+bx+c一定与x轴有两个交点,
∴c<0.
点评:本题考查的是反比例函数综合题,涉及到矩形与菱形的性质、二次函数的性质等知识,难度较大.

练习册系列答案
相关题目
下列事件发生的概率为0的是( )
| A、随意掷一枚均匀的硬币两次,至少有一次反面朝上 |
| B、今年冬天黑龙江会下雪 |
| C、随意掷两个均匀的骰子,朝上面的点数之和为1 |
| D、一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域 |
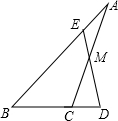 如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=
如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=| 1 |
| 4 |
| A、2:1 | B、3:2 |
| C、3:1 | D、5:2 |
 已知四边形ABCD中,AB=CD,AD=CB,求证:AD∥BC.
已知四边形ABCD中,AB=CD,AD=CB,求证:AD∥BC.