题目内容
已知物品甲每个3元,乙每个1.5元,丙每个0.25元.现甲乙丙三样物品都要买,共55元全部用完,要买40个,则一共有多少种方案?
考点:二元一次方程的应用
专题:
分析:根据题意设购买每个3元的x个,每个1.5元的y个,进而利用甲乙丙三样物品都要买,共55元全部用完得出等式进而分析即可.
解答:解:设购买每个3元的x个,每个1.5元的y个,
则购买每个0.25元的(40-x-y)个.
由题意得3x+1.5y+0.25(40-x-y)=55;
化简得2.75x+1.25y=45;
∵x和y是正整数,
∴x=10;y=14或x=15;y=3;
∴方案一:购买每个3元的10个,每个1.5元的14个,每个0.25元的16个.
方案二:购买每个3元的15个,每个1.5元的3个,每个0.25元的22个.
则购买每个0.25元的(40-x-y)个.
由题意得3x+1.5y+0.25(40-x-y)=55;
化简得2.75x+1.25y=45;
∵x和y是正整数,
∴x=10;y=14或x=15;y=3;
∴方案一:购买每个3元的10个,每个1.5元的14个,每个0.25元的16个.
方案二:购买每个3元的15个,每个1.5元的3个,每个0.25元的22个.
点评:此题主要考查了二元一次方程的应用,得出正确等量关系是解题关键.

练习册系列答案
相关题目
美国NBA职业篮球赛的两支队伍在本赛季已进行了5场比赛,根据统计,两队5场比赛得分的频数分布直方图如下所示,则得分方差较小的队伍是( )


| A、甲 | B、乙 | C、一样大 | D、无法确定 |
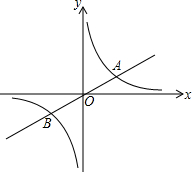 反比例函数y=
反比例函数y= 已知点A、B、C在⊙O上,连接AB、AC、BC,若∠A=90°,求证:BC为⊙O的直径.
已知点A、B、C在⊙O上,连接AB、AC、BC,若∠A=90°,求证:BC为⊙O的直径.