题目内容
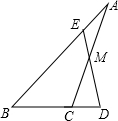如图，在△ABC中，M是AC边中点，E是AB上一点，且AE=| 1 |
| 4 |
| A、2：1 | B、3：2 |
| C、3：1 | D、5：2 |
考点：平行线分线段成比例
专题：
分析：过点M作MF∥BC交AB于F，然后判断出MF是△ABC的中位线，再求出BF=
AB，再求出EF=
AB，再根据平行线分线段成比例定理可得
=
．
| 1 |
| 2 |
| 1 |
| 4 |
| DM |
| EM |
| BF |
| EF |
解答：
解：如图，过点M作MF∥BC交AB于F，
∵M是AC边中点，
∴MF是△ABC的中位线，
∴BF=
AB，
∵AE=
AB，
∴EF=AB-
AB-
AB=
AB，
又∵MF∥BC，
∴
=
=2，
即DM：EM=2：1．
故选A．
解：如图，过点M作MF∥BC交AB于F，∵M是AC边中点，
∴MF是△ABC的中位线，
∴BF=
| 1 |
| 2 |
∵AE=
| 1 |
| 4 |
∴EF=AB-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
又∵MF∥BC，
∴
| DM |
| EM |
| BF |
| EF |
即DM：EM=2：1．
故选A．
点评：本题考查了平行线分线段成比例定理，三角形的中位线平行于第三边并且等于第三边的一半，熟记定理并作出辅助线是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
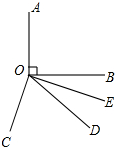如图所示，OA⊥OB，OC⊥OE，OD为∠BOC的平分线，∠BOE=16°，求∠DOE的度数．
如图，正六边形ABCDEF中．阴影部分面积为12
反比例函数y=