题目内容
17.正方形ABCD的面积为(2-$\sqrt{3}$)cm2,点P是对角线AC上一动点,则线段AP,BP,DP之和的最小值为1cm.分析 将△APD绕点A逆时针旋转60°得到△AFE,连接BE交AC于点G,连接PF、DE,则△APF、△ADE是等边三角形,从而得出PA+PB+PD=PF+PB+EF,进而得出∠BAE=∠BAD+∠DAE=150°,得出∠ABE=∠AEB=15°,即可求得∠AQE=∠BAC+∠ABE=60°,证得PF∥BE,设直线AF交BE于点G,则△AQG是等边三角形,当P运动到Q处时,点F运动到G处,此时折线B-P-F-E变成线段BE,此时PA+PB+PD取得最小值BE,设正方形的面积为a2=2-$\sqrt{3}$,则EH=$\frac{a}{2}$,AH=$\frac{\sqrt{3}}{2}$a,根据勾股定理得出BE2=BH2+EH2=(a+$\frac{\sqrt{3}}{2}$a)2+($\frac{a}{2}$)2=(2+$\sqrt{3}$)a2=(2+$\sqrt{3}$)(2-$\sqrt{3}$)=1,即可求得PA+PB+PD的最小值为1.
解答  解:如图所示:将△APD绕点A逆时针旋转60°得到△AFE,连接BE交AC于点G,连接PF、DE,则△APF、△ADE是等边三角形,
解:如图所示:将△APD绕点A逆时针旋转60°得到△AFE,连接BE交AC于点G,连接PF、DE,则△APF、△ADE是等边三角形,
∴PA+PB+PD=PF+PB+EF,
∵AB=AD=AE,∠BAE=∠BAD+∠DAE=150°,
∴∠ABE=∠AEB=15°,
∴∠AQE=∠BAC+∠ABE=60°,
∴PF∥BE,
设直线AF交BE于点G,则△AQG是等边三角形,
∴当P运动到Q处时,点F运动到G处,此时折线B-P-F-E变成线段BE,
∴PA+PB+PD=PF+PB+EF≥BE,
即P运动到Q处PA+PB+PD取得最小值BE,
设正方形的面积为a2=2-$\sqrt{3}$,则EH=$\frac{a}{2}$,AH=$\frac{\sqrt{3}}{2}$a,
∴BE2=BH2+EH2=(a+$\frac{\sqrt{3}}{2}$a)2+($\frac{a}{2}$)2=(2+$\sqrt{3}$)a2=(2+$\sqrt{3}$)(2-$\sqrt{3}$)=1,
∴PA+PB+PD的最小值为1.
故答案为1.
点评 本题考查了正方形的性质,等边三角形的判定和性质,勾股定理的应用,轴对称-最短路线问题,两点之间线段最短是解题的关键.

 阅读快车系列答案
阅读快车系列答案 已知:如图,AB=CD,AD=BC,求证:AB∥CD,AD∥BC.
已知:如图,AB=CD,AD=BC,求证:AB∥CD,AD∥BC.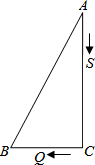 如图,△ABC中,∠C=90°,AB=5,BC=3.S、Q两点同时分别从A、C出发,点S以每秒2个单位的速度沿着AC向点C运动,点Q以每秒1个单位的速度沿着CB向点B运动,当其中一点到达终点时,另一点也随之停止移动.
如图,△ABC中,∠C=90°,AB=5,BC=3.S、Q两点同时分别从A、C出发,点S以每秒2个单位的速度沿着AC向点C运动,点Q以每秒1个单位的速度沿着CB向点B运动,当其中一点到达终点时,另一点也随之停止移动.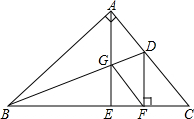 如图,在△ABC中,∠BAC=90°,在BC上截取BF=BA,作DF⊥BC交AC于D点,AE⊥BC于E点,交BD于G点,连接GF,求证:DG平分∠AGF.
如图,在△ABC中,∠BAC=90°,在BC上截取BF=BA,作DF⊥BC交AC于D点,AE⊥BC于E点,交BD于G点,连接GF,求证:DG平分∠AGF. 如图,△ABC的边BC、AC为一边作等边△BCD和等边△ACE,连结DE.试猜想DE和AB的数量关系并证明.
如图,△ABC的边BC、AC为一边作等边△BCD和等边△ACE,连结DE.试猜想DE和AB的数量关系并证明.