题目内容
6. 如图,△ABC的边BC、AC为一边作等边△BCD和等边△ACE,连结DE.试猜想DE和AB的数量关系并证明.
如图,△ABC的边BC、AC为一边作等边△BCD和等边△ACE,连结DE.试猜想DE和AB的数量关系并证明.
分析 DE=AB,根据SAS证明△EDC≌△ABC即可得出DE=AB.
解答 解:DE=AB.
理由:∵△BCD和△ACE都是等边三角形,
∴CE=CA,CD=CB,∠ECA=∠BCD=60°,
∵∠BCE=60°+∠ACB=60°+∠ECD,
∴∠ACB=∠ECD,
在△EDC和△ABC中,
$\left\{\begin{array}{l}{CE=CA}\\{∠ACB=∠ECD}\\{CD=CB}\end{array}\right.$,
∴△EDC≌△ABC,
∴DE=AB.
点评 本题主要考查了全等三角形的判定与性质以及等边三角形的性质,熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
1.下列方程中,是关于x的一元二次方程的有( )
| A. | x(2x-1)=2x2 | B. | $\frac{1}{x^2}$-2x=1 | C. | ax2+bx+c=0 | D. | $\frac{1}{2}$x2=0 |
 一个由若干个小正方体搭建而成的几何体的三视图如图,则搭建这个几何体的小正方体有8个.
一个由若干个小正方体搭建而成的几何体的三视图如图,则搭建这个几何体的小正方体有8个. 画出下面几何体的从正面、从左面、从上面看到的形状图.
画出下面几何体的从正面、从左面、从上面看到的形状图.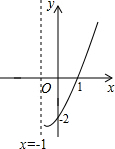 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( ) 玻璃三角板摔成三块如图,若到玻璃店在配一块同样大小的三角板,最省事的方法带③.
玻璃三角板摔成三块如图,若到玻璃店在配一块同样大小的三角板,最省事的方法带③.