Question

4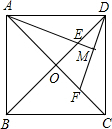．如图，在正方形ABCD中，对角线AC、BD相交于点O，E、F分别在OD、OC上，且DE=CF，连接DF、AE，AE的延长线交DF于点M．猜想线段AE与线段DF的关系并证明你的猜想．

Answer 1

分析 根据DE=CF，可得出OE=OF，继而证明△AOE≌△DOF，得出AE=DF，由△AOE≌△DOF得出∠OAE=∠ODF，然后利用等角代换可得出∠DME=90°，得出结论．

解答 解：线段AE与线段DF的关系是相等且垂直，
∵四边形ABCD是正方形，
∴CO=DO，
又∵DE=CF，
∴OD-DE=OC-CF，即OF=OE，
在△AOE和△DOF中，
$\left\{\begin{array}{l}{AO=DO}\\{∠AOD=∠DOF}\\{OE=OF}\end{array}\right.$，
∴△AOE≌△DOF（SAS），
∴AE=DF，
∵△AOE≌△DOF，
∴∠OAE=∠ODF，
∵∠OAE+∠AEO=90°，∠AEO=∠DEM，
∴∠ODF+∠DEM=90°，
即AE⊥DF．

点评 此题考查了正方形的性质、全等三角形的判定与性质，解答本题的关键是通过全等的证明和利用等角代换解题．