题目内容
10．已知，函数y=$\frac{k}{x}$的图象经过点（-1，2），则函数y=kx+2的图象不经过（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 先求出k的值，再由一次函数的图象与系数的关系即可得出结论．
解答 解：∵函数y=$\frac{k}{x}$的图象经过点（-1，2），
∴k=（-1）×2=-2，
∴函数y=kx+2的解析式为y=-2x+2，
∵k=-2＜0，b=2＞0，
∴函数图象经过一、二、四象限，不经过第三象限．
故选C．
点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
18．
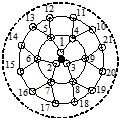课题研究小组对附着在物体表面的三个微生物（课题小组成员把他们分别标号为1，2，3）的生长情况进行观察记录．这三个微生物第一天各自一分为二，产生新的微生物（分别被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录）．那么标号为150的微生物会出现在（ ）
课题研究小组对附着在物体表面的三个微生物（课题小组成员把他们分别标号为1，2，3）的生长情况进行观察记录．这三个微生物第一天各自一分为二，产生新的微生物（分别被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录）．那么标号为150的微生物会出现在（ ）| A． | 第3天 | B． | 第4天 | C． | 第5天 | D． | 第6天 |
5．若顺次连接四边形的各边中点所得的四边形是菱形，则该四边形一定是（ ）
| A． | 矩形 | B． | 菱形 | ||
| C． | 对角线相等的四边形 | D． | 对角线互相垂直的四边形 |
解不等式：$\frac{x-1}{6}-\frac{x}{3}＞-\frac{1}{2}$，并将解集在数轴上表示出来．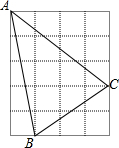
阅读：直角三角形具有下列性质，若直角三角形的两直角分别为a，b．斜边为c，则a2+b2=c2，利用这一性质．可求出某些线段的长，如图，正方形网格中，每个小正方形的边长均为1，则BC2=22+32，即BC=$\sqrt{2^2+3^2}$=$\sqrt{13}$，因3$＜\sqrt{13}＜$4，所以线段BC的长是无理数，请你利用以上阅读材料，判断图中线段AC、AB的长是有理数还是无理数，并说明理由．