题目内容
12.把二次函数y=-$\frac{1}{4}$x2-x+3配方化为y=a(x-h)2+k形式( )| A. | y=-$\frac{1}{4}$(x-2)2+2 | B. | y=-$\frac{1}{4}$(x-2)2+4 | C. | y=-$\frac{1}{4}$(x+2)2+4 | D. | y=-$\frac{1}{4}$(x-1)2+3 |
分析 利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式.
解答 解:y=-$\frac{1}{4}$x2-x+3
=-$\frac{1}{4}$(x2+4x+4)+3+1
=-$\frac{1}{4}$(x+2)2+4,
即y=-$\frac{1}{4}$(x+2)2+4.
故选:C.
点评 本题考查了二次函数的性质及二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
3.若x2-3x+1=0,则x4+$\frac{1}{{x}^{4}}$的个位数字是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
7.下列等式由左到右的变形是因式分解的是( )
| A. | a2-b2+1=(a+b)(a-b)+1 | B. | xy(x2+y2)(x+y)(x-y)=x5y-xy5 | ||
| C. | (m+3)2=m2+9 | D. | x2-9=(x+3)(x-3) |
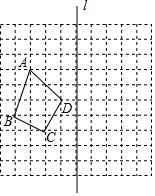 请你在所给的网格中画出四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于直线l对称.
请你在所给的网格中画出四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于直线l对称.
 如图,在△ABC中,∠ACB=90°,正方形DEFG的顶点D,E分别在边AC、BC上,顶点F、G都在边AB上.
如图,在△ABC中,∠ACB=90°,正方形DEFG的顶点D,E分别在边AC、BC上,顶点F、G都在边AB上.