题目内容
4. 如图,在△ABC中,∠ACB=90°,正方形DEFG的顶点D,E分别在边AC、BC上,顶点F、G都在边AB上.
如图,在△ABC中,∠ACB=90°,正方形DEFG的顶点D,E分别在边AC、BC上,顶点F、G都在边AB上.(1)求证:GF2=AG•BF;
(2)若△ABC的面积为48,AB=12,求正方形DEFG的边长.
分析 (1)根据相似三角形的判定定理得出△ADG∽△EBF,由相似三角形的对应边成比例即可得出结论;
(2)过点C作过C作CH⊥AB交DE于M,设正方形DEFG的边长为x,根据△ABC的面积为48,AB=12,得到CH=8,根据相似三角形的性质即可得到结论.
解答 解:(1)∵四边形DEFG是正方形,
∴DG=GF=EF,∠DGF=∠EFG=90°,
∴∠DGA=∠EFB=90°,
∴∠A+∠B=∠FEB+∠B=90°,
∴∠A=∠FEB,
∴△AGD∽△EFB,
∴$\frac{AG}{EF}=\frac{DG}{BF}$,
即$\frac{AG}{GF}=\frac{GF}{BF}$,
∴GF2=AG•BF;
(2)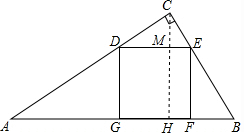 过C作CH⊥AB交DE于M,
过C作CH⊥AB交DE于M,
设正方形DEFG的边长为x,
∵△ABC的面积为48,AB=12,
∴CH=8,
∵DE∥AB,
∴CM⊥DE,△CDE∽△CAB,
∴$\frac{CM}{CH}$=$\frac{DE}{AB}$,
即$\frac{8-x}{8}$=$\frac{x}{12}$,
∴x=$\frac{24}{5}$,
∴正方形DEFG的边长为$\frac{24}{5}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
12.把二次函数y=-$\frac{1}{4}$x2-x+3配方化为y=a(x-h)2+k形式( )
| A. | y=-$\frac{1}{4}$(x-2)2+2 | B. | y=-$\frac{1}{4}$(x-2)2+4 | C. | y=-$\frac{1}{4}$(x+2)2+4 | D. | y=-$\frac{1}{4}$(x-1)2+3 |
19.下列代数式中,不是分式的是( )
| A. | $\frac{x}{x}$ | B. | 1-$\frac{1}{x}$ | C. | $\frac{1}{x+y}$ | D. | x+$\frac{2a}{3}$ |
9.如果一个四边形绕对角线的交点旋转90°后,所得图形与原来的图形重合,那么这个四边形是( )
| A. | 正方形 | B. | 菱形 | ||
| C. | 矩形 | D. | 对角线垂直的任意四边形 |
16.若|a|=8,|b|=5,且a>0,b<0,a-b的值是( )
| A. | 3 | B. | -3 | C. | 13 | D. | -13 |
11.有理数-7的相反数是( )
| A. | -$\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | 7 | D. | ±7 |
 已知:抛物线y=ax2+bx+c的图象如图所示,则a的取值范围是a<0.
已知:抛物线y=ax2+bx+c的图象如图所示,则a的取值范围是a<0.