题目内容
已知关于x的方程x2+3x-m=0有两个实数根,并且这两个实数根的平方和为11,求m的值.
考点:根与系数的关系,根的判别式
专题:
分析:设方程的两根分别为a、b,根据根与系数的关系得到a+b=-3,ab=-m,由于a2+b2=11,根据完全平方公式得到(a+b)2-2ab=11,则(-3)2-2(-m)=11,解得m=1,然后利用根的判别式确定m的值.
解答:解:设方程的两根分别为a、b,则a+b=-3,ab=-m,
∵a2+b2=11,
∴(a+b)2-2ab=11,
∴(-3)2-2(-m)=11,
解得m=1,
当m=1时,原方程变形为x2+3x-1=0,△=9-4×(-1)=13>0,方程有两个不相等的实数根,
∴m的值为1.
∵a2+b2=11,
∴(a+b)2-2ab=11,
∴(-3)2-2(-m)=11,
解得m=1,
当m=1时,原方程变形为x2+3x-1=0,△=9-4×(-1)=13>0,方程有两个不相等的实数根,
∴m的值为1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1x2=
,也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
 已知:如图,在△ABC中,对于以下的四个论断:
已知:如图,在△ABC中,对于以下的四个论断: 在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,AD=2,DC=11,求AB和BC的长.
在四边形ABCD中,∠A=∠C=90°,∠ADC=120°,AD=2,DC=11,求AB和BC的长.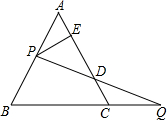 如图,边长为1的等边△ABC中,一动点P沿AB从A向B移动,动点Q以同样的速度从C出发沿BC的延长线运动,连PQ交AC边于D,作PE⊥AC于E,则DE的长为
如图,边长为1的等边△ABC中,一动点P沿AB从A向B移动,动点Q以同样的速度从C出发沿BC的延长线运动,连PQ交AC边于D,作PE⊥AC于E,则DE的长为