题目内容
17.有一列数a1,a2,a3,…,an,满足下列条件:a1=0,|a2|=|a1+1|,|a3|=|a2+1|,…,|an|=|an-1+1|.求证:a1,a2,a3,…,an这n个数的算术平均数不小于$-\frac{1}{2}$.分析 首先把|a2|=|a1+1|,|a3|=|a2+1|,…,|an|=|an-1+1|两边平方,再相加整理得出答案即可.
解答 证明:∵a1=0,|a2|=|a1+1|,|a3|=|a2+1|,…,|an|=|an-1+1|,
∴a12=0,a22=(a1+1)2,a32=(a2+1)2,…,an2=(an-1+1)2,
即a12=0,a22=a12+2a1+1,a32=a22+2a2+1,…,an2=an-12+2an-1+1,
∴a12+a22+a32+…+an2=a12+2a1+1+a22+2a2+1+…+an-12+2an-1+1,
∴2(a1+a2+a3+…+an)=an2-n≥-n,
∴$\frac{1}{n}$(a1+a2+a3+…+an)≥$-\frac{1}{2}$,
即a1,a2,a3,…,an这n个数的算术平均数不小于$-\frac{1}{2}$.
点评 此题考查算术平方数,掌握恒等变形与求算术平均数的方法是解决问题的关键.

练习册系列答案
相关题目
8.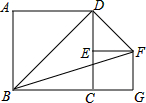 如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )
如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )
 如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )
如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
2. 如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
 如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |

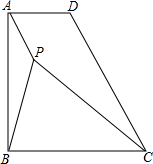 已知在直角梯形ABCD中,∠ABC=90°,AB=BC,点P是梯形内一点,且PA=1,PB=2,PC=3
已知在直角梯形ABCD中,∠ABC=90°,AB=BC,点P是梯形内一点,且PA=1,PB=2,PC=3 已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2).
已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2). 如图,P为菱形ABCD的对角线AC上一点,若PB=3,则PD=3.(填“>”或“=”或“<”号)
如图,P为菱形ABCD的对角线AC上一点,若PB=3,则PD=3.(填“>”或“=”或“<”号)