题目内容
1.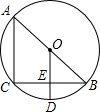 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC、BD.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC、BD.(1)请写出两个不同类型的正确结论.
(2)若CB=2$\sqrt{2}$,BD=$\sqrt{3}$,求⊙O的半径.
分析 (1)根据直角所对的圆周角是直角、垂径定理写出结论;
(2)根据勾股定理求出DE的长,设⊙O的半径为R,根据勾股定理列出关于R的方程,解方程得到答案.
解答 解:(1)∵AB是⊙O的直径,
∴∠C=90°,
∵OD⊥CB,
∴CE=BE,
则两个不同类型的正确结论:∠C=90°;CE=BE;
(2)∵OD⊥CB,
∴CE=BE=$\frac{1}{2}$BC=$\sqrt{2}$,又BD=$\sqrt{3}$,
∴DE=$\sqrt{B{D}^{2}-B{E}^{2}}$=1,
设⊙O的半径为R,则OE=R-1,
∴R2=(R-1)2+($\sqrt{2}$)2,
解得R=$\frac{3}{2}$.
答:⊙O的半径为$\frac{3}{2}$.
点评 本题考查的是垂径定理和勾股定理的应用,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )
如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )
 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )
如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )| A. | △ADC≌△BDH | B. | HE=EC | C. | AH=BD | D. | △AHE≌△BHD |
13.精确到十分位( )
| A. | 13.42 | B. | 134.20 | C. | 1.342 | D. | 1342.0 |
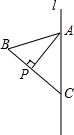 如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.
如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.