题目内容
2.已知直线$y=\frac{1}{2}x$与反比例函数$y=\frac{k}{x}(k>0)$图象交于A,B两点,点A坐标为(4,m),点P是反比例函数图象上的一动点,过P、O作直线OP,与反比例函数图象的另一交点为Q.(1)求k的值;
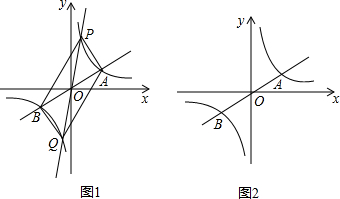
(2)如图1,若点P的纵坐标为8,求四边形APBQ的面积;
(3)点P在运动过程中,是否存在以点P为顶点的矩形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)利用待定系数法将x=4代入$y=\frac{1}{2}x$得y的值,进而可得A点坐标,再把A的坐标代入反比例函数可得k的值;
(2)过P作PD⊥x轴,作AE⊥x轴,首先求出P点坐标,再根据S△AOP=S△POD+S梯形AEDC-S△AOE代入数据可得△APO的面积,再根据平行四边形的性质可得S平行四边形APBQ=4S△AOP可得答案;
(3)当点P在第一象限时,分别过点A、P作x轴,y轴的垂线AM、PN,然后证出△OAM≌△OPN,求出P点坐标,再根据当点P在第三象限时,点P坐标即可.
解答  解:(1)将x=4代入$y=\frac{1}{2}x$得:y=2,
解:(1)将x=4代入$y=\frac{1}{2}x$得:y=2,
故A(4,2),
把A点坐标代入$y=\frac{k}{x}(k>0)$可得k=8;
(2)过P作PD⊥x轴,作AE⊥x轴,
将y=8代入反比例函数解析式得:x=1,
即P(1,8),
∴DO=1,PD=8,
∵A(4,2),
∴EO=4,AE=2,
∵S△AOP=S△POD+S梯形AEDC-S△AOE=$\frac{1}{2}×1×8$+$\frac{1}{2}×$(2+8)-$\frac{1}{2}×4×2$=15,
又由双曲线的对称性可知,四边形APBQ为平行四边形,
∴S平行四边形APBQ=4S△AOP=4×15=60,
(3)当点P在第一象限时,如图2,
分别过点A、P作x轴,y轴的垂线AM、PN,
∵四边形APBQ为矩形,
∴AO=OP,
由双曲线关于一、三象限角平分线对称,
∴△OAM与△OPN关于一、三象限角平分线对称,
∴△OAM≌△OPN,
∴ON=OM=4,PN=AM=2,
∴点P的坐标为(2,4),
同理可得,当点P在第三象限时,点P坐标为(-2,-4),
综上,P点坐标为(2,4)(-2,-4).
点评 此题主要考查了反比例函数综合,关键是掌握凡是函数经过的点必能满足解析式,平行四边形对角线把平行四边形分成四个面积相等的三角形.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
| A. | -(+5)和+(-5) | B. | -(-5)和+(-5) | C. | -(+5)和-5 | D. | +(-5)和-5 |
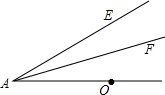 如图,AF平分∠OAE,M是射线AF上一动点,N是线段AO上一动点,判断是否存在点M、N.使得OM+NM的值最小?若存在,请画出M、N点,并加以说明:若不存在,请说明理由.
如图,AF平分∠OAE,M是射线AF上一动点,N是线段AO上一动点,判断是否存在点M、N.使得OM+NM的值最小?若存在,请画出M、N点,并加以说明:若不存在,请说明理由.
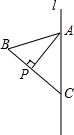 如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.
如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.