题目内容
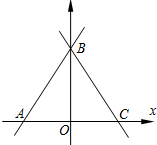 如图,直线y=
如图,直线y=| 3 |
| 3 |
考点:一次函数综合题
专题:
分析:当P点在AO之间运动时,作QH⊥x轴.再求得QH,从而求得三角形APQ的面积,进而得出当△APQ的面积最大时,t的值,得出Q,B重合,进而利用菱形的性质求出即可.
解答:解:∵直线y=
x+4
与x轴、y轴分别交于A、B两点,
∴x=0,y=4
,y=0,x=-4,
∴A点坐标为:(-4,0),AO=4,BO=4
,
∴AB=8,
∴∠BAC=60°,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴CO=4,BC=8,
当P点在AO之间运动时,作QH⊥x轴.
∵
=
,
∴
=
,
∴QH=
t
∴S△APQ=
AP•QH=
t•
t=
t2﹙0<t≤4﹚,
同理可得S△APQ=
t•﹙8
-
t﹚=-
t2+4
t﹙4≤t<8﹚,
当t=4时S=
t2,S=-
t2+4
t此时取到最大值,
∴当△APQ的面积最大时,此时Q与B重合,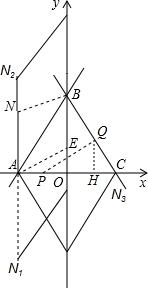
当以A、Q、M、N为顶点的四边形为菱形,
AN1=8时,且AN1∥y轴,则N1(-4,-8),
AN2=8时,且AN2∥y轴,则N2(-4,8),
当N3点与C点重合坐标为:N3(4,0),
当AB是对角线,AE=AN=BE,设BE=x,则AE=AN=x,
∴在Rt△AEO中
AE2=EO2+AO2,
∴x2=(4
-x)2+42,
解得:x=
,
∴N(-4,
),
综上所述,点N的坐标为:(4,0)(-4,8)或(-4,-8)或(-4,
).
故答案为:(4,0)(-4,8)或(-4,-8)或(-4,
).
| 3 |
| 3 |
∴x=0,y=4
| 3 |
∴A点坐标为:(-4,0),AO=4,BO=4
| 3 |
∴AB=8,
∴∠BAC=60°,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴CO=4,BC=8,
当P点在AO之间运动时,作QH⊥x轴.
∵
| QH |
| OB |
| CQ |
| CB |
∴
| QH | ||
4
|
| 2t |
| 8 |
∴QH=
| 3 |
∴S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
同理可得S△APQ=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
当t=4时S=
| ||
| 2 |
| ||
| 2 |
| 3 |
∴当△APQ的面积最大时,此时Q与B重合,

当以A、Q、M、N为顶点的四边形为菱形,
AN1=8时,且AN1∥y轴,则N1(-4,-8),
AN2=8时,且AN2∥y轴,则N2(-4,8),
当N3点与C点重合坐标为:N3(4,0),
当AB是对角线,AE=AN=BE,设BE=x,则AE=AN=x,
∴在Rt△AEO中
AE2=EO2+AO2,
∴x2=(4
| 3 |
解得:x=
8
| ||
| 3 |
∴N(-4,
8
| ||
| 3 |
综上所述,点N的坐标为:(4,0)(-4,8)或(-4,-8)或(-4,
8
| ||
| 3 |
故答案为:(4,0)(-4,8)或(-4,-8)或(-4,
8
| ||
| 3 |
点评:此题主要考查了菱形的性质以及三角形面积求法和勾股定理等知识,利用数形结合以及分类讨论得出N的位置是解题关键.

练习册系列答案
相关题目
 如图,AD∥BC,∠D=90°,AD=2,BC=5,DC=11.若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )
如图,AD∥BC,∠D=90°,AD=2,BC=5,DC=11.若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )| A、1个 | B、2个 | C、3个 | D、4个 |
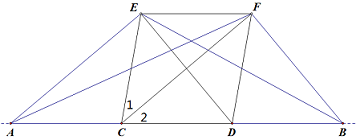 如图,点C,D在线段AB上,EF∥AB,CE=CD,∠1=∠2.
如图,点C,D在线段AB上,EF∥AB,CE=CD,∠1=∠2. 如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于
如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于