题目内容
16. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
分析 (1)根据三角形中位线定理得MN=$\frac{1}{2}$AD,根据直角三角形斜边中线定理得BM=$\frac{1}{2}$AC,由此即可证明.
(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
解答 (1)证明:在△CAD中,∵M、N分别是AC、CD的中点,
∴MN∥AD,MN=$\frac{1}{2}$AD,
在RT△ABC中,∵M是AC中点,
∴BM=$\frac{1}{2}$AC,
∵AC=AD,
∴MN=BM.
(2)解:∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=30°,
由(1)可知,BM=$\frac{1}{2}$AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MN∥AD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,
由(1)可知MN=BM=$\frac{1}{2}$AC=1,
∴BN=$\sqrt{2}$
点评 本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
7.已知方程x-2y+3=8,则整式x-2y的值为( )
| A. | 5 | B. | 10 | C. | 12 | D. | 15 |
4.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
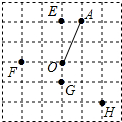

| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
11.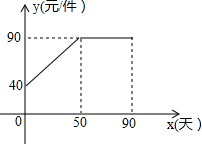 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元). | 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
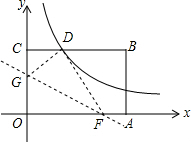 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.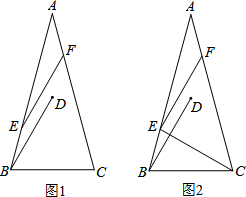 在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上. 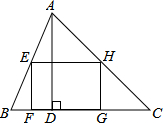 如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.
如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.