题目内容
4.定义:[a,b]为反比例函数$y=\frac{a}{bx}$(ab≠0,a,b为实数)的“关联数”. 反比例函数$y=\frac{k_1}{x}$的“关联数”为[m,m+2],反比例函数$y=\frac{k_2}{x}$的“关联数”为[m+1,m+3],若m>0,则( )| A. | k1=k2 | B. | k1>k2 | C. | k1<k2 | D. | 无法比较 |
分析 利用题中的新定义表示出k1与k2,利用作差法比较即可.
解答 解:根据题意得:$\left\{\begin{array}{l}{{k}_{1}=\frac{m}{m+2}}\\{{k}_{2}=\frac{m+1}{m+3}}\end{array}\right.$,
∵m>0,
∴k1-k2=$\frac{m}{m+2}$-$\frac{m+1}{m+3}$=$\frac{{m}^{2}+3m-{m}^{2}-3m-2}{(m+2)(m+3)}$=-$\frac{2}{(m+2)(m+3)}$<0,
则k1<k2.
点评 此题考查了反比例函数的定义,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
13.下列各式计算正确的是( )
| A. | 3x2•4x3=12x6 | B. | 3x3•(-2x2)=-6x5 | C. | (-3x2)•(5x3)=15x5 | D. | (-2x)2•(-3x)3=6x5 |
18.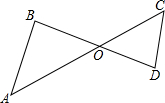 如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
 如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )| A. | $\frac{OB}{OC}$=$\frac{OA}{OD}$ | B. | $\frac{OA}{OB}$=$\frac{OD}{OC}$ | C. | $\frac{OA}{OD}$=$\frac{AB}{CD}$ | D. | $\frac{OC}{OB}$=$\frac{OD}{OA}$ |

 甲、乙两专卖店日销售收入y元和x天的函数图象如图,在这期间,乙店停业装修一段时间,重新开业后,乙店的日均销售收入是原来的2倍,则下列说法中正确的为( )
甲、乙两专卖店日销售收入y元和x天的函数图象如图,在这期间,乙店停业装修一段时间,重新开业后,乙店的日均销售收入是原来的2倍,则下列说法中正确的为( )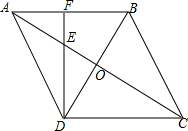 如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB.
如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB.