题目内容
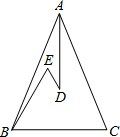 如图,在△ABC中,∠ABC=∠C,∠EBC=∠BED=60°,AD平分∠BAC,求证:∠D=30°.
如图,在△ABC中,∠ABC=∠C,∠EBC=∠BED=60°,AD平分∠BAC,求证:∠D=30°.考点:等边三角形的判定与性质,等腰三角形的性质
专题:
分析:延长ED、AD分别交BC与点G、F,利用等腰三角形的三线合一得出∠DFG=90°,利用等边三角形的性质得出∠DGF=60°,根据三角形的内角和得出∠FDG,对顶角相等得出结论.


解答:证明:如图,

延长ED、AD分别交BC与点G、F,
∵∠ABC=∠C,
∴△ABC为等腰三角形,
∵AD平分∠BAC,
∴AF⊥BC,
即∠DFG=90°,
∵∠EBC=∠BED=60°,
∴∠DGF=60°,
∴∠EDA=∠GDF=30°.

延长ED、AD分别交BC与点G、F,
∵∠ABC=∠C,
∴△ABC为等腰三角形,
∵AD平分∠BAC,
∴AF⊥BC,
即∠DFG=90°,
∵∠EBC=∠BED=60°,
∴∠DGF=60°,
∴∠EDA=∠GDF=30°.
点评:此题考查等腰三角形的判定与性质,等边三角形的判定与性质,利用已知条件作出辅助线是解决问题的关键.

练习册系列答案
相关题目
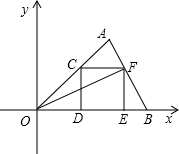 如图,在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
如图,在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
 如图,若平移梯形ABCD的一条对角线,使平移后的这条对角线与图中的其它某些线段(含线段的延长线)构成一个三角形,则能否构成一个面积恰好等于梯形面积的三角形?若能,请你说说应该如何构造?
如图,若平移梯形ABCD的一条对角线,使平移后的这条对角线与图中的其它某些线段(含线段的延长线)构成一个三角形,则能否构成一个面积恰好等于梯形面积的三角形?若能,请你说说应该如何构造? 如图,水库大坝的截面是梯形ABCD,坝顶AD=4m,高度为2m.tanB=
如图,水库大坝的截面是梯形ABCD,坝顶AD=4m,高度为2m.tanB=