题目内容
14. 如图,在△ABC中,AB=AC,BC=6,AD=4,E,F是中线AD上的两点,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC,BC=6,AD=4,E,F是中线AD上的两点,则图中阴影部分的面积是( )| A. | 6 | B. | 12 | C. | 24 | D. | 30 |
分析 根据等腰三角形性质求出BD=DC,AD⊥BC,推出△CEF和△BEF关于直线AD对称,得出S△BEF=S△CEF,根据图中阴影部分的面积是$\frac{1}{2}$S△ABC求出即可.
解答 解:∵AB=AC,BC=6,AD是△ABC的中线,
∴BD=DC=$\frac{1}{2}$BC=3,AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×6×4=12,
∴图中阴影部分的面积是$\frac{1}{2}$S△ABC=6.
故选A.
点评 本题考查了等腰三角形的性质,轴对称的性质.通过观察可以发现是轴对称图形,且阴影部分的面积为全面积的一半,根据轴对称图形的性质求解.其中看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知a,b是方程x2-6x+4=0的两实数根,且a≠b,则$\frac{b}{a}$+$\frac{a}{b}$的值是( )
| A. | 7 | B. | -7 | C. | 11 | D. | -11 |
5.已知点A(-2,y1),B(2,y2),C(3,y3)在抛物线y=x2-2x+c上,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y3>y1 |
2.“$\frac{9}{16}$的算术平方根是$\frac{3}{4}$”,用数学式子表示为( )
| A. | ±$\sqrt{\frac{9}{16}}$=$\frac{3}{4}$ | B. | $\sqrt{\frac{9}{16}}$=±$\frac{3}{4}$ | C. | $\sqrt{\frac{9}{16}}$=$\frac{3}{4}$ | D. | ±$\sqrt{\frac{9}{16}}$=±$\frac{3}{4}$ |
19.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a2016的值为( )
| A. | -1006 | B. | -1007 | C. | -1008 | D. | -2016 |
4.在直角坐标系中,已知点A(1,0),⊙A的半径是5,若点D(-2,a)在⊙A外,则a的范围是( )
| A. | a>4 | B. | a>4或a<-4 | C. | a<-4 | D. | -4<a<4 |
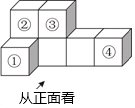 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )
如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )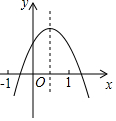 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④a-c>0.其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④a-c>0.其中正确结论的个数为( ) 如图,在△ABC中,AB=3,AC=4,BC=5,P为BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为2.4.
如图,在△ABC中,AB=3,AC=4,BC=5,P为BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为2.4.