题目内容
 如图,已知△ABC,AB=AC,∠BAC=90°,D为CB延长线上一点,连AD,以AD为边在△ABC的同侧作正方形ADEF.
如图,已知△ABC,AB=AC,∠BAC=90°,D为CB延长线上一点,连AD,以AD为边在△ABC的同侧作正方形ADEF.(1)求证:∠EBD=45°;
(2)求
| 2DC-BC |
| EB |
(3)若AF=2,AC=
| 2 |
考点:全等三角形的判定与性质,勾股定理,正方形的性质
专题:
分析:(1)如图1,作AM⊥DC于M,EN⊥DC于N,由正方形的性质就可以得出∠NED=∠MDA,得出△END≌△DMA,就有EN=DM.ND=MA,得出NB=EN而得出结论;
(2)如图2,作AM⊥DC于M,EN⊥DC于N,作EP⊥EB于E,交CB的延长线于P,可以得出∠P=45°,就有PN=NB=DM,而ND=BM=MC,PN+ND=DM+MC,∴PC=2DC,在Rt△PEB中,∠EBD=45°,由勾股定理就可以得出PB=
BE,而2CD-BC=PB,从而得出结论;
(3)如图3,连接BF,作AM⊥DC于M,EN⊥DC于N,正方形和等腰直角三角形的性质就可以得出△FAB≌△DAC,由勾股定理就可以得出AM=BM=CM=1,DM=
,就可以求出正方形AFED的面积和△ADC的面积和,求出△EDB和△ABC的面积就可以得出结论.
(2)如图2,作AM⊥DC于M,EN⊥DC于N,作EP⊥EB于E,交CB的延长线于P,可以得出∠P=45°,就有PN=NB=DM,而ND=BM=MC,PN+ND=DM+MC,∴PC=2DC,在Rt△PEB中,∠EBD=45°,由勾股定理就可以得出PB=
| 2 |
(3)如图3,连接BF,作AM⊥DC于M,EN⊥DC于N,正方形和等腰直角三角形的性质就可以得出△FAB≌△DAC,由勾股定理就可以得出AM=BM=CM=1,DM=
| 3 |
解答:解:(1)如图1,作AM⊥DC于M,EN⊥DC于N,
∴∠END=∠DMA=90°.
∴∠DEN+∠NDE=90°.
∵四边形AFED是正方形,
∴ED=DA=AF,∠EDA=∠DAF=90°.
∴∠EDN+∠ADM=90°,
∴∠NED=∠MDA.
在△END和△DMA中,
,
∴△END≌△DMA(AAS),
∴EN=DM.ND=MA.
∵AB=AC,∠BAC=90°,AM⊥BC,
∴AM=BM=MC,
∴ND=BM,
∴ND+BD=BM+BD,
∴NB=DM,
∴NB=EN,
∴∠EBD=45°;
(2)如图2,作AM⊥DC于M,EN⊥DC于N,作EP⊥EB于E,交CB的延长线于P,
∴∠PEB=90°,
∴∠P=∠EBD=45°.
∵EN⊥BP,
∴PN=NB=EN.
∵EN=DM,
∴PN=DM.
∵ND=BM=MC,
∴PN+ND=DM+MC,
∴PD=DC,
∴PC=2DC.
在Rt△PEB中,∠EBD=45°,
∴PB=
BE.
∵2DC-BC=PC-BC,
∴2DC-BC=PB=
BE,
∴
=
;
(3)如图3,连接BF,作AM⊥DC于M,EN⊥DC于N,
∴∠END=∠DMA=90°.
∴∠DEN+∠NDE=90°.
∵四边形AFED是正方形,
∴ED=DA=AF,∠EDA=∠DAF=90°.
∴∠EDN+∠ADM=90°,
∴∠NED=∠MDA.
在△END和△DMA中,
,
∴△END≌△DMA(AAS),
∴EN=DM.
∵∠BAC=90°,
∴∠FAD=∠BAC,
∴∠FAD+∠DAB=∠BAC+∠DAB,
∴∠FAB=∠DAC.
在△FAB和△DAC中,
,
∴△FAB≌△DAC(SAS),
∴S△FAB=S△DAC.
∵∠BAC=90°,AB=AC=
,由勾股定理,得
BC=2.
∵AM⊥BC,
∴BM=CM=AM=1.
∵AD=2,在Rt△ADM中,由勾股定理,得
DM=
.
∴EN=
,DB=
-1,DC=
+1.
∴S△ADC=
,S△EDB=
=
,S△ABC=
=1
∴S△FAB=
.
∵AF=2,
∴S正方形AFED=4.
∵S△EBF=S正方形AFED+S△DAC-S△ABC-S△FAB-S△EDB,
=4+
-
-1-
=
.
故答案为:
.
∴∠END=∠DMA=90°.
∴∠DEN+∠NDE=90°.
∵四边形AFED是正方形,
∴ED=DA=AF,∠EDA=∠DAF=90°.
∴∠EDN+∠ADM=90°,
∴∠NED=∠MDA.
在△END和△DMA中,
|
∴△END≌△DMA(AAS),
∴EN=DM.ND=MA.
∵AB=AC,∠BAC=90°,AM⊥BC,

∴AM=BM=MC,
∴ND=BM,
∴ND+BD=BM+BD,
∴NB=DM,
∴NB=EN,
∴∠EBD=45°;
(2)如图2,作AM⊥DC于M,EN⊥DC于N,作EP⊥EB于E,交CB的延长线于P,
∴∠PEB=90°,

∴∠P=∠EBD=45°.
∵EN⊥BP,
∴PN=NB=EN.
∵EN=DM,
∴PN=DM.
∵ND=BM=MC,
∴PN+ND=DM+MC,
∴PD=DC,
∴PC=2DC.
在Rt△PEB中,∠EBD=45°,
∴PB=
| 2 |
∵2DC-BC=PC-BC,
∴2DC-BC=PB=
| 2 |
∴
| 2DC-BC |
| EB |
| 2 |
(3)如图3,连接BF,作AM⊥DC于M,EN⊥DC于N,
∴∠END=∠DMA=90°.
∴∠DEN+∠NDE=90°.
∵四边形AFED是正方形,
∴ED=DA=AF,∠EDA=∠DAF=90°.
∴∠EDN+∠ADM=90°,
∴∠NED=∠MDA.
在△END和△DMA中,
|
∴△END≌△DMA(AAS),
∴EN=DM.
∵∠BAC=90°,
∴∠FAD=∠BAC,
∴∠FAD+∠DAB=∠BAC+∠DAB,
∴∠FAB=∠DAC.

在△FAB和△DAC中,
|
∴△FAB≌△DAC(SAS),
∴S△FAB=S△DAC.
∵∠BAC=90°,AB=AC=
| 2 |
BC=2.
∵AM⊥BC,
∴BM=CM=AM=1.
∵AD=2,在Rt△ADM中,由勾股定理,得
DM=
| 3 |
∴EN=
| 3 |
| 3 |
| 3 |
∴S△ADC=
| ||
| 2 |
| ||||
| 2 |
3-
| ||
| 2 |
| 2×1 |
| 2 |
∴S△FAB=
| ||
| 2 |
∵AF=2,
∴S正方形AFED=4.
∵S△EBF=S正方形AFED+S△DAC-S△ABC-S△FAB-S△EDB,
=4+
| ||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了等腰直角三角形的性质的运用,正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,正方形的面积公式,三角形的面积公式的运用,解答时灵活运用等腰直角三角形的性质求解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 图中几何体的俯视图是( )
图中几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
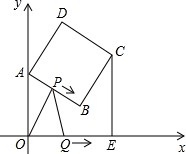 如图,在正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限,动点P在正方形ABCD的边上从点A出发沿A→B→C以每秒一个单位长度匀速运动,同时动点Q以每秒
如图,在正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限,动点P在正方形ABCD的边上从点A出发沿A→B→C以每秒一个单位长度匀速运动,同时动点Q以每秒 如图,已知⊙P和⊙O 相交于A、G两点,AB是⊙O的直径,且交⊙P于点E,⊙O的弦CD过点E,且CD⊥AB交⊙P于F,FA与⊙O交于M,且F、G、B三点在一条直线上,GE的延长线交⊙O于N,连结AN.
如图,已知⊙P和⊙O 相交于A、G两点,AB是⊙O的直径,且交⊙P于点E,⊙O的弦CD过点E,且CD⊥AB交⊙P于F,FA与⊙O交于M,且F、G、B三点在一条直线上,GE的延长线交⊙O于N,连结AN.