题目内容
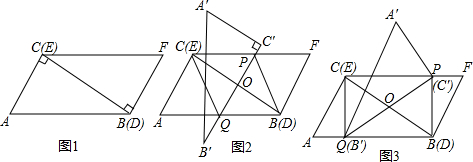
12.Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板,按如图1所示拼在一起,CB与DE重合.(1)四边形ABFC是平行四边形吗?为什么?
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转90°到如图2中的△A′B′C′位置,直线B′C′与AB、CF分别相交于Q、P两点,猜想四边形CQBP的形状,并说明理由;
(3)在(2)的条件下,将△ABC绕点O顺时钟方向继续旋转到如图3中的△A′B′C′位置,请说明四边形CQBP是什么类型的四边形,并求出∠COP的度数.
分析 (1)证明AC∥BF且AC=BF即可证得;
(2)首先证明△PCO≌△QBO证得OP=OQ,然后根据菱形的定义证得;
(3)首先证明四边形CQBP是平行四边形,然后根据等边对等角求得∠OPC的度数,进而求解.
解答 解:(1)四边形ABFC是平行四边形.
∵∠ACB=∠EDF=90°,
∴AC∥BF,
∵AC=BF,
∴四边形ABFC是平行四边形;
(2)四边形CQBP是菱形.
∵AB∥CF,
∴∠CPQ=∠PQB,
在△PCO和△QBO中,
$\left\{\begin{array}{l}{∠CPQ=∠PQB}\\{∠PCB=∠CBQ}\\{OC=OB}\end{array}\right.$,
又∵∠PCB=∠CBQ=30°,OC=OB,
∴△PCO≌△QBO,
∴OP=OQ,
∴四边形CQBP是平行四边形.
∵∠COP=90°
∴四边形CQBP是菱形.
(3)∵△PCO≌△QBO,OP=OQ
∴四边形CQBP是平行四边形,
又∵CB=PQ
∴四边形CQBP是矩形.
∵OC=OP,∠OCP=30°
∴∠OPC=30°
∴∠COP=180°-∠COP-∠OPC=120°.
点评 本题考查了全等三角形判定,正确证明四边形ABFC是平行四边形是关键.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
2.如果$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程x-3y=-3的一组解,那么代数式5-a+3b的值是( )
| A. | 8 | B. | 5 | C. | 2 | D. | 0 |
17.如果a=(-2016)0,b=($\frac{1}{2}$)-1,c=(-3)-2,那么a、b、c的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | c>a>b |
6.如图,函数y1=ax+b与y2=bx+a正确的图象为( )
| A. |  | B. |  | C. |  | D. |  |
 如图,四边形ABCD是菱形,点E,点F分别是CD,AD上的点,CE=DF,DE=2CE,AE,CF交于点O,则AO:OE=6.
如图,四边形ABCD是菱形,点E,点F分别是CD,AD上的点,CE=DF,DE=2CE,AE,CF交于点O,则AO:OE=6. 如图,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,则∠FDE=70°.
如图,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,则∠FDE=70°.