题目内容
 将图中的△ABC作下列运动,画出相应的图形
将图中的△ABC作下列运动,画出相应的图形(1)沿y轴向下平移3个单位;
(2)关于y轴对称;
(3)以点A为位似中心,放大到2倍得到△AB′C′,并写出A、B′、C′三点的坐标.
考点:作图-位似变换,作图-轴对称变换,作图-平移变换
专题:几何变换
分析:(1)先根据点平移的规律写出点A、B、C平移后对应点的坐标,即A1(-3,-4),B1(-2,-2),C1(0,-5),然后描点后依次连结A1、B1、C1即可;
(2)先根据关于y轴对称的点的坐标特征写出点A、B、C关于y轴对称的对应点的坐标,即A2(3,-1),B2(2,1),C2(0,2),然后描点后依次连结A2、B2、C2即可;
(3)根据位似图形的画法,分别延长AB到B′点,使AB′=2AB,延长AC到C′点,使AC′=2AC,连结B′C′,则△AB′C′为所求,然后写出A、B′、C′三点的坐标.
(2)先根据关于y轴对称的点的坐标特征写出点A、B、C关于y轴对称的对应点的坐标,即A2(3,-1),B2(2,1),C2(0,2),然后描点后依次连结A2、B2、C2即可;
(3)根据位似图形的画法,分别延长AB到B′点,使AB′=2AB,延长AC到C′点,使AC′=2AC,连结B′C′,则△AB′C′为所求,然后写出A、B′、C′三点的坐标.
解答: 解:(1)∵A(-3,-1),B(-2,1),C(0,-2),
解:(1)∵A(-3,-1),B(-2,1),C(0,-2),
∴△ABC沿y轴向下平移3个单位得到各对应点的坐标为A1(-3,-4),B1(-2,-2),C1(0,-5),
依次连结A1、B1、C1得到△A1B1C1,如图;
(2)点A(-3,-1),B(-2,1),C(0,-2)分别关于y轴对称的对应点的坐标为A2(3,-1),B2(2,1),C2(0,2),依次连结A2、B2、C2得到△A2B2C2,如图;
(3)延长AB到B′点,使AB′=2AB,延长AC到C′点,使AC′=2AC,连结B′C′,则△AB′C′为所求,A(-3,-1),B′(-1,3),C′(3,-3).
 解:(1)∵A(-3,-1),B(-2,1),C(0,-2),
解:(1)∵A(-3,-1),B(-2,1),C(0,-2),∴△ABC沿y轴向下平移3个单位得到各对应点的坐标为A1(-3,-4),B1(-2,-2),C1(0,-5),
依次连结A1、B1、C1得到△A1B1C1,如图;
(2)点A(-3,-1),B(-2,1),C(0,-2)分别关于y轴对称的对应点的坐标为A2(3,-1),B2(2,1),C2(0,2),依次连结A2、B2、C2得到△A2B2C2,如图;
(3)延长AB到B′点,使AB′=2AB,延长AC到C′点,使AC′=2AC,连结B′C′,则△AB′C′为所求,A(-3,-1),B′(-1,3),C′(3,-3).
点评:本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;然后根据位似比,确定能代表所作的位似图形的关键点;最后顺次连接上述各点,得到放大或缩小的图形.也考查了轴对称变换与平移变换.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,在下列四个几何体中,它的三视图(主视图、左视图、俯视图)完全相同的是 ( )


| A、①② | B、②③ | C、①④ | D、②④ |
 如图,在⊙O中,弦AB,AC互相垂直,D,E分别为AB,AC的中点,则四边形OEAD为( )
如图,在⊙O中,弦AB,AC互相垂直,D,E分别为AB,AC的中点,则四边形OEAD为( )| A、正方形 | B、菱形 |
| C、矩形 | D、直角梯形 |
轴对称图形的对称轴的条数有( )
| A、1条 | B、2条 |
| C、至少有1条 | D、3条 |
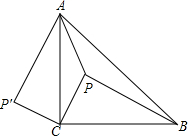 如图,P是等腰Rt△ACB内一点,AC=BC,且PA=8,PB=10,PC=
如图,P是等腰Rt△ACB内一点,AC=BC,且PA=8,PB=10,PC=