题目内容
4.先化简,后求值:($\frac{{x}^{2}y-4{y}^{3}}{{x}^{2}+4xy+4{y}^{2}}$)•($\frac{4xy}{x-2y}$+x),其中x=$\sqrt{2}$-1,y=$\sqrt{2}+1$.分析 首先对括号内的分式进行分解因式,对后边括号内的式子进行通分相加,然后进行约分即可化简,然后代入数值计算即可.
解答 解:原式=$\frac{y(x+2y)(x-2y)}{(x+2y)^{2}}$•$\frac{4xy+{x}^{2}-2xy}{x-2y}$
=$\frac{y(x+2y)(x-2y)}{(x+2y)^{2}}$•$\frac{x(x+2y)}{x-2y}$
=xy.
当x=$\sqrt{2}$-1,y=$\sqrt{2}$+1时,原式=($\sqrt{2}$-1)($\sqrt{2}$+1)=1.
点评 本题考查了分式的化简求值,正确对式子进行通分、约分是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
15.下列分式的值,可以为零的是( )
| A. | $\frac{{x}^{2}+1}{x-1}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | C. | $\frac{{x}^{2}+2x+1}{x+1}$ | D. | $\frac{x+1}{x-1}$ |
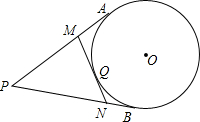 如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.
如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.