Question

19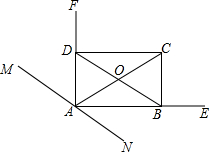．如图所示，AF是∠MAC角平分线，AE是∠NAC的角平分线，OB=OD，且OA=OC，求证：四边形ABCD为矩形．

Answer 1

分析 只要证明四边形ABCD是平行四边形，再证明∠DAB=90°即可．

解答 证明：∵AF是∠MAC角平分线，AE是∠NAC的角平分线，
∴∠CAF=$\frac{1}{2}$∠CAM，∠CAB=$\frac{1}{2}$∠CAN，
∴∠CAF+∠CAB=$\frac{1}{2}$（∠CAM+∠CAN）=90°，即∠DAB=90°
∵OD=OB，OA=OC，
∴四边形ABCD是平行四边形，
∵∠DAB=90°，
∴四边形ABCD是矩形．

点评 本题考查角平分线的定义，矩形的判定、平行四边形的判定等知识，解题的关键是熟练掌握基本概念，属于直径基础题．