题目内容
11.(1)(-1)2017+(-$\frac{1}{3}$)-1+$|{-\sqrt{2}}|$-2sin45°.(2)先化简,再求值:$\frac{x-3}{x-2}$÷(x+2-$\frac{5}{x-2}$),其中x=$\sqrt{2}$-3.
分析 (1)首先计算乘方、去掉绝对值符号、代入特殊角的三角函数值,然后进行加减计算即可;
(2)首先把括号内的分式通分相加,把除法转化为乘法,计算乘法即可化简,最后代入数值计算即可.
解答 解:(1)原式=-1+(-3)+$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$
=-1-3+$\sqrt{2}$-$\sqrt{2}$
=-4;
(2)原式=$\frac{x-3}{x-2}$÷$\frac{(x+2)(x-2)-5}{x-2}$
=$\frac{x-3}{x-2}$•$\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{x+3}$,
当x=$\sqrt{2}$-3时,原式=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了实数的运算和分式的化简求值,正确对分式进行通分、约分是关键.

练习册系列答案
相关题目
1.下列各式计算正确的是( )
| A. | x2•x3=x6 | B. | 2x+3x=5x2 | C. | x6÷x2=x3 | D. | (x2)3=x6 |
2.学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:
则得分的众数和中位数分别为( )
| 得分(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 7 | 12 | 10 | 8 | 3 |
| A. | 70分,70分 | B. | 80分,80分 | C. | 70分,80分 | D. | 80分,70分 |
19.若α、β是方程x2-3x-2017=0的两个实数根,则代数式α2-2β-5α的值为( )
| A. | -2011 | B. | -2023 | C. | 2011 | D. | 2023 |
6.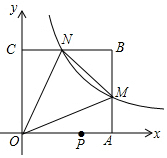 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )| A. | 6$\sqrt{2}$ | B. | 10 | C. | 2$\sqrt{26}$ | D. | 2$\sqrt{29}$ |
16. 一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )
一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )
 一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )
一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )| A. | 中 | B. | 考 | C. | 顺 | D. | 利 |
 七(1)班举行投篮比赛,每人投5球.如图是全班学生投进球数的扇形统计图,则投进球数的众数是3球.
七(1)班举行投篮比赛,每人投5球.如图是全班学生投进球数的扇形统计图,则投进球数的众数是3球.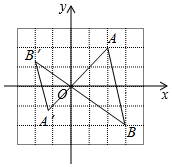 如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是(-2,$\frac{4}{3}$).
如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是(-2,$\frac{4}{3}$).