题目内容
16. 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )| A. | 汽车在行驶途中停留了0.5小时 | |
| B. | 汽车在行驶途中的平均速度为$\frac{80}{3}$千米/小时 | |
| C. | 汽车共行驶了240千米 | |
| D. | 汽车自出发后3小时至4.5小时之间行驶的速度是80千米/小时 |
分析 根据函数图形的s轴判断行驶的总路程,从而得到C正确;根据s不变时为停留时间判断出A正确;根据平均速度=总路程÷总时间列式计算即可判断出C错误;再根据一次函数图象的实际意义判断出D正确.
解答 解:A汽车在行驶途中停留了2-1.5=0.5小时,故本小题正确;
B汽车在整个行驶过程中的平均速度为$\frac{240}{4.5}=\frac{160}{3}$千米/时,故本小题错误;
C由图可知,汽车共行驶了120×2=240千米,故C正确;
D汽车自出发后3小时至4.5小时之间行驶离出发地越来越近,是匀速运动,速度是80千米/小时,故本小题正确;
故选B.
点评 本题考查了一次函数的应用,主要利用了路程、速度、时间三者之间的关系,准确识图,理解转折点的实际意义是解题的关键.

练习册系列答案
相关题目
7.下列说法正确的是( )
| A. | 一个数的相反数一定比0小 | |
| B. | 互为相反数的两个数的绝对值相等 | |
| C. | 一个数的绝对值一定是正数 | |
| D. | 若两个数的绝对值相等,则这两个数相等 |
4.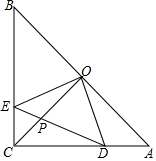 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论
(1)△AOD≌△COE;(2)OE=OD;(3)△EOP∽△CDP.
其中正确的结论是( )
 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论(1)△AOD≌△COE;(2)OE=OD;(3)△EOP∽△CDP.
其中正确的结论是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
11.一个圆柱侧面展开后是一个正方形,这个圆柱的底面半径与高的比是( )
| A. | 1:π | B. | 1:2π | C. | π:1 | D. | 2π:1 |
1.下列命题中,错误的是( )
| A. | 两条对角线相等的平行四边形是矩形 | |
| B. | 两条对角线互相垂直的四边形是菱形 | |
| C. | 两条对角线互相垂直的矩形是正方形 | |
| D. | 两条对角线互相平分的四边形是平行四边形 |
8.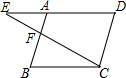 如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则与△AEF相似的三角形有( )
如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则与△AEF相似的三角形有( )
 如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则与△AEF相似的三角形有( )
如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则与△AEF相似的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.小明一家人在国庆期间自驾汽车从家里出发到某著名旅游景点游玩,他在1:500000的地图上测得家所在城市与旅游景点所在城市的图上距离为40cm,则这两城市的实际距离为( )
| A. | 100km | B. | 200km | C. | 1000km | D. | 2000km |
 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,则BD:AB=1:4.
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,则BD:AB=1:4.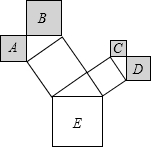 如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( )
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( )