题目内容
4.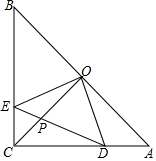 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论(1)△AOD≌△COE;(2)OE=OD;(3)△EOP∽△CDP.
其中正确的结论是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据等腰直角三角形的性质,以及直角三角形斜边中线定理首先证明△AOD≌△COE(ASA),推出OE=OD,∠OED=∠PCD=45°即可解决问题.
解答 解:∵在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,
∴∠A=∠B=∠ACO=45°,OA=OC=OB,∠AOC=90°=∠DOE,
∴∠AOD=∠COE=90°-∠DOC,
在△AOD与△COE中,
$\left\{\begin{array}{l}{∠OAD=∠OCE}\\{OA=OC}\\{∠AOD=∠COE}\end{array}\right.$,
∴△AOD≌△COE(ASA),
∴OD=OE,故①②正确,
∵∠EOD=90°,
∴∠OED=45°,
∵∠ACB=90°,BC=AC,OB=OA,
∴∠PCD=∠PCE=45°,
∴∠OEP=∠DCP,∵∠EPO=∠CPD,
∴△△EOP∽△CDP,故③正确,
故选D.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形的条件,以及三角形相似的条件,属于基础题,中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若点P(2m-1,3)在第二象限,则m的取值范围是( )
| A. | m>$\frac{1}{2}$ | B. | m<$\frac{1}{2}$ | C. | m$≥\frac{1}{2}$ | D. | m$≤\frac{1}{2}$ |
12. 如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )
如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )
 如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )
如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )| A. | S△MNQ=$\frac{1}{2}$MN•PQ | B. | ∠MQT=∠MQP | C. | MT=MP | D. | ∠NQP=∠MQT |
9.比较-2,-$\frac{1}{2}$,0,0.02的大小,正确的是( )
| A. | -$\frac{1}{2}$<-2<0.02<0 | B. | -$\frac{1}{2}$<-2<0<0.02 | C. | -2<-$\frac{1}{2}$<0.02<0 | D. | -2<-$\frac{1}{2}$<0<0.02 |
16. 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )
 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )| A. | 汽车在行驶途中停留了0.5小时 | |
| B. | 汽车在行驶途中的平均速度为$\frac{80}{3}$千米/小时 | |
| C. | 汽车共行驶了240千米 | |
| D. | 汽车自出发后3小时至4.5小时之间行驶的速度是80千米/小时 |
13.一个点从数轴上的原点出发,向左移动3个单位长度,再向右移动2个单位长度到达点P,则点P表示的数是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
14.随机掷一枚质地均匀的硬币两次,落地后两次都是反面朝上的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )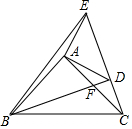 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一条直角形上,连接B、D和B,E,下列四个结论:
如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一条直角形上,连接B、D和B,E,下列四个结论: