题目内容
6.甲、乙、丙三人每分分别行60米、50米和40米,甲从B地、乙和丙从A地同时出发相向而行,途中甲遇到乙后15分钟又遇到丙,求A、B两地的距离.分析 甲遇到乙后15分钟又遇到丙,则从甲遇到乙后,再和丙相遇的这15分钟里,甲丙共行了(60+40)×15=1500米,即甲乙相遇时,乙比丙多行了1500米,乙丙两人的速度差为:50-40=10(米/分钟),则甲乙相遇时,乙行了1500÷10=150分钟,所以A、B两地的距离为:(60+50)×150=110×150=16500(米),据此解答即可.
解答 解:(60+40)×15÷(50-40)×(60+50)
=100×15÷10×110
=150×110
=16500(米).
答:A、B两地相距16500米.
点评 此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出甲乙的相遇时间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.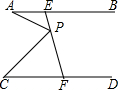 如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )
如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )
 如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )
如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
14.在“我为震灾献爱心”的捐赠活动中,某班40位同学捐款金额统计如下:
则这次活动中,该班同学捐款金额的众数是50;中位数是50;平均数是55.
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 3 | 6 | 6 | 15 | 10 |
11.若x1、x2是一元二次方程x2-4x-3=0的两个根,则x1+x2的值是( )
| A. | -4 | B. | 4 | C. | 3 | D. | -3 |
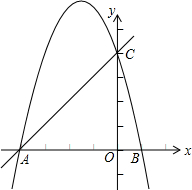 如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).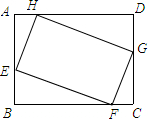 如图,矩形ABCD中,AB=3,BC=4,E、F、G、H分别在四边上,且四边形EFGH为矩形,若EF=2EH,则AE=$\frac{5}{3}$.
如图,矩形ABCD中,AB=3,BC=4,E、F、G、H分别在四边上,且四边形EFGH为矩形,若EF=2EH,则AE=$\frac{5}{3}$.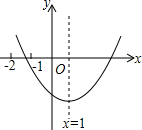 已知二次函数y=ax2+bx+c(a≠0)≠的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a-b=0;④8a+c<0;⑤9a+3b+c<0.其中结论正确的个数有( )
已知二次函数y=ax2+bx+c(a≠0)≠的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a-b=0;④8a+c<0;⑤9a+3b+c<0.其中结论正确的个数有( )