题目内容
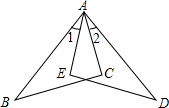 如图,已知AB=AD,∠B=∠D,∠1=∠2,说明:BC=DE.
如图,已知AB=AD,∠B=∠D,∠1=∠2,说明:BC=DE.考点:全等三角形的判定与性质
专题:证明题
分析:由∠1=∠2可推出∠BAC=∠DAE,再由已知条件结合三角形的判定方法即可证明△BAC≌△DAE,利用全等三角形的性质可得:BC=DE.
解答:证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(AAS),
∴BC=DE.
∴∠1+∠EAC=∠2+∠EAC,
即∠BAC=∠DAE,
在△BAC和△DAE中,
|
∴△BAC≌△DAE(AAS),
∴BC=DE.
点评:本题考查了全等三角形的判定和性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
 如图,过原点的直线分别交双曲线y=
如图,过原点的直线分别交双曲线y=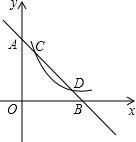 如图,
如图, 如图,直线AB与CD相交于点O,OE⊥AB,∠COE=30°,求∠DOA的度数.
如图,直线AB与CD相交于点O,OE⊥AB,∠COE=30°,求∠DOA的度数. 如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,OA=8,OC=6.反比例函数y1=
如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,OA=8,OC=6.反比例函数y1=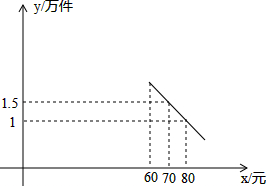 某企业在自主研制新产品的同时考虑招聘员工的计划,已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元,设产品月销售量为y(万件),销售单价为x(元),试销阶段40≤x≤60,企业把试销情况列成表格(见下表),正式销售阶段60<x<100,企业把销售情况绘制成函数关系(见下图).
某企业在自主研制新产品的同时考虑招聘员工的计划,已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元,设产品月销售量为y(万件),销售单价为x(元),试销阶段40≤x≤60,企业把试销情况列成表格(见下表),正式销售阶段60<x<100,企业把销售情况绘制成函数关系(见下图).

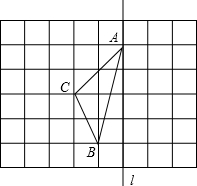 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.