题目内容
3.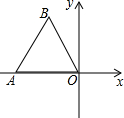 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )| A. | (2,2$\sqrt{3}$) | B. | (-2,4) | C. | (-2,2$\sqrt{2}$) | D. | (-2,2$\sqrt{3}$) |
分析 作BC⊥x轴于C,如图,根据等边三角形的性质得OA=OB=4,AC=OC=2,∠BOA=60°,则易得A点坐标和O点坐标,再利用勾股定理计算出BC=2$\sqrt{3}$,然后根据第二象限点的坐标特征可写出B点坐标;由旋转的性质得∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,则点A′与点B重合,于是可得点A′的坐标.
解答 解:作BC⊥x轴于C,如图,
∵△OAB是边长为4的等边三角形
∴OA=OB=4,AC=OC=1,∠BOA=60°,
∴A点坐标为(-4,0),O点坐标为(0,0),
在Rt△BOC中,BC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴B点坐标为(-2,2$\sqrt{3}$);
∵△OAB按顺时针方向旋转60°,得到△OA′B′,
∴∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,
∴点A′与点B重合,即点A′的坐标为(-2,2$\sqrt{3}$),
故选:D.
点评 本题考查了坐标与图形变化-旋转:记住关于原点对称的点的坐标特征;图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°;解决本题的关键是正确理解题目,按题目的叙述一定要把各点的大致位置确定,正确地作出图形.

练习册系列答案
相关题目
13.下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
| A. | a=6,b=8,c=10 | B. | a=5,b=12,c=13 | C. | a=1,b=2,c=3 | D. | a=3,b=4,c=5 |
11.点A(-1,y1)和点B(3,y2)在反比例函数y=-$\frac{1}{x}$图象上,则y1与y2的大小关系是( )
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
18.地球上水的总储量约为1.39×1018立方米,但目前能被人们生产、生活利用的水只占总储量的0.77%,因此我们要节约用水,那么用科学记数法表示能被人们生产、生活利用的水约为( )
| A. | 1.0703×1015立方米 | B. | 1.0703×1016立方米 | ||
| C. | 1.0703×1017立方米 | D. | 1.0703×1018立方米 |
8.下列说法中不正确的是( )
| A. | 抛掷一枚质量均匀的硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉至少有两个球是必然事件 | |
| C. | 任意打开八年级下册数学教科书,正好是97页是确定事件 | |
| D. | 从一副扑克牌中任意抽取1张,摸到的牌是“A”的可能性比摸到的牌是“红桃”可能性小 |
15.下列函数中,y是x的正比例函数的是( )
| A. | y=2x+1 | B. | $y=\frac{x}{3}$ | C. | y=2x2 | D. | $y=\frac{3}{x}$ |
12.菱形的周长是16cm,菱形的高是2cm,则菱形其中一个内角的角度是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
