题目内容

1．有一人患了流感，经过两轮传染后共有111人患了流感，每轮传染中平均一个人传染的人数为（　　）
A．12B．11C．10D．9

分析 设每轮传染中平均一个人传染的人数为x，则第一轮传染后共有（x+1）人患了流感，找出第二轮传染后患流感的人数即可得出关于x的一元二次方程，解之即可得出结论．

解答 解：设每轮传染中平均一个人传染的人数为x，则第一轮传染后共有（x+1）人患了流感，
根据题意得：x（x+1）=111，
解得：x=10或x=-11（舍去）．
故选C．

点评 本题考查了一元二次方程的应用以及列代数式，根据经过两轮传染后共有111人患了流感列出关于x的一元二次方程是解题的关键．

练习册系列答案
相关题目
11．下列条件能判定△ABC为等腰三角形的是（　　）
A．∠A=30°，∠B=60°B．AB=5，AC=12，BC=13
C．∠A=50°，∠B=80°D．∠A：∠B：∠C=3：4：5
12．下列计算正确的是（　　）
A．a2•a3=a6B．（a2）3=a5C．（-2ab）2=4a2b2D．3a2b2÷a2b2=3ab
9．计算：（-$\frac{1}{2}$）-2+（-2017）0=5．
16．已知：a=2014x+2015，b=2014x+2016，c=2014x+2017，则a2+b2+c2-ab-ac-bc的值是（　　）
A．0B．1C．2D．3
6．若kb＞0，则函数y=kx+b的图象可能是（　　）
A．B．C．D．
13．在（$\frac{\sqrt{5}-1}{2}$）0，|-$\frac{2}{3}$|，tan30°，10-2这几个实数中，最大的实数是（$\frac{\sqrt{5}-1}{2}$）0．
15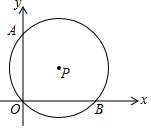．如图，⊙P与两条坐标轴分别交于点A、O、B，若点A、B的坐标分别为（0，6）、（8，0），则圆心P的坐标为（　　）
A．（4，3）B．（3，4）C．（3，3）D．（4，4）
16．（1）化简：（$\frac{1}{3}$x+$\frac{3}{4}$y）（$\frac{1}{3}$x-$\frac{3}{4}$y）-（$\frac{1}{3}$x-$\frac{3}{4}$y）
（2）先化简，在求值：（4ab3-8a2b2）÷4ab+（2a+b）（2a-b），其中a=2，b=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网