题目内容
13.在($\frac{\sqrt{5}-1}{2}$)0,|-$\frac{2}{3}$|,tan30°,10-2这几个实数中,最大的实数是($\frac{\sqrt{5}-1}{2}$)0.分析 首先利用零指数幂、绝对值、特殊角的三角函数值和负整数指数幂的计算法则计算,再根据实数大小比较的方法进行比较即可求解.
解答 解:∵($\frac{\sqrt{5}-1}{2}$)0=1,|-$\frac{2}{3}$|=$\frac{2}{3}$,tan30°=$\frac{\sqrt{3}}{3}$,10-2=$\frac{1}{100}$,
1>$\frac{2}{3}$>$\frac{\sqrt{3}}{3}$>$\frac{1}{100}$,
∴最大的实数是($\frac{\sqrt{5}-1}{2}$)0.
故答案为:($\frac{\sqrt{5}-1}{2}$)0.
点评 此题主要考查了实数大小比较,实数运算以及零指数幂、绝对值、特殊角的三角函数值和负整数指数幂,正确化简各数是解题关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
3.在0,-2,(-3)0,-(-5)在四个数中,最小的数是( )
| A. | -2 | B. | 0 | C. | (-3)0 | D. | -(-5) |
4.-3的绝对值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
1.有一人患了流感,经过两轮传染后共有111人患了流感,每轮传染中平均一个人传染的人数为( )
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
8.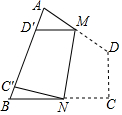 如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
 如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
3.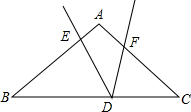 如图,AB=AC,∠B=∠EDF,DE=3,BE=4,CD=3.则DF的长为( )
如图,AB=AC,∠B=∠EDF,DE=3,BE=4,CD=3.则DF的长为( )
 如图,AB=AC,∠B=∠EDF,DE=3,BE=4,CD=3.则DF的长为( )
如图,AB=AC,∠B=∠EDF,DE=3,BE=4,CD=3.则DF的长为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{9}{4}$ | D. | 3 |
8.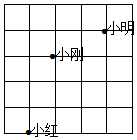 如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
 如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )| A. | (0,0) | B. | (0,1) | C. | (1,0) | D. | (1,1) |